题目内容

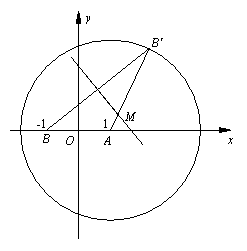
已知点为圆：上任意一点，点B(-1,0)，线段的垂直平分线和线段相交于点M.

（1）求点M的轨迹E的方程；

（2）已知点为曲线E上任意一点，求证：点关于直线的对称点为定点，并求出该定点的坐标.

解：

（1）连结MB，,

故，而                             -------------------------4分

点M的轨迹是以A、B为焦点且长轴长为的椭圆

点M的轨迹E的方程为                          ------------------------8分

（2）证明：设点关于直线的对称点为

所以，即            ----------------------10分

，

                                     -------------------------14分

因为上式对任意成立，故

所以对称点为定点.                                 -------------------------16分

练习册系列答案
相关题目
已知点P是圆M：x2+（y+m）2=8（m＞0，m≠
2
）上一动点，点N（0，m）是圆M所在平面内一定点，线段NP的垂直平分线l与直线MP相交于点Q．
（Ⅰ）当P在圆M上运动时，记动点Q的轨迹为曲线Γ，判断曲线Γ为何种曲线，并求出它的标准方程；
（Ⅱ）过原点斜率为k的直线交曲线Γ于A，B两点，其中A在第一象限，且它在y轴上的射影为点C，直线BC交曲线Γ于另一点D，记直线AD的斜率为k′．是否存在m，使得对任意的k＞0，都有|k•k′|=1？若存在，求m的值；若不存在，请说明理由．
（2013•牡丹江一模）已知双曲线E：
x2
a2
-
y2
b2
=1的焦距为4，以原点为圆心，实半轴长为半径的圆和直线x-y+
6
=0相切．
（Ⅰ） 求双曲线E的方程；
（Ⅱ）已知点F为双曲线E的左焦点，试问在x轴上是否存在一定点M，过点M任意作一条直线l交双曲线E于P，Q两点，使
FP
•
FQ
为定值？若存在，求出此定值和所有的定点M的坐标；若不存在，请说明理由．
（2013•宝山区一模）已知半径为R的球的球面上有三个点，其中任意两点间的球面距离都等于
πR
3
，且经过这三个点的小圆周长为4π，则R=
2
3
2
3
．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
（A）（几何证明选做题）已知PA是圆D的切线，切点为A，PA=2，AC是圆D的直径，PC与圆D交于点B，PB=1，则圆O的半径r=
3
3
．
（B）（极坐标系与参数方程选做题）在极坐标系中，曲线p=4cos（θ-
π
3
）上任意两点间的距离的最大值为
4
4
．
（C）（不等式选做题）若不等式|x-2|+|x+1|≥α对于任意x∈R恒成立，则实数a的取值范围为
{α|α≤3}
{α|α≤3}
．

已知点为圆上的动点，且不在轴上，轴，垂足为，线段中点的轨迹为曲线，过定点任作一条与轴不垂直的直线，它与曲线交于、两点。

（I）求曲线的方程；

（II）试证明：在轴上存在定点，使得总能被轴平分

【解析】第一问中设为曲线上的任意一点，则点在圆上，

∴，曲线的方程为

第二问中，设点的坐标为，直线的方程为，　　………………3分　 　

代入曲线的方程，可得　

∵，∴

确定结论直线与曲线总有两个公共点．

然后设点,的坐标分别, ，则，  

要使被轴平分，只要得到。

（1）设为曲线上的任意一点，则点在圆上，

∴，曲线的方程为．  ………………2分       

（2）设点的坐标为，直线的方程为，　　………………3分　 　

代入曲线的方程，可得　，……5分            

∵，∴，

∴直线与曲线总有两个公共点．（也可根据点M在椭圆的内部得到此结论）

………………6分

设点,的坐标分别, ，则，   

要使被轴平分，只要，            ………………9分

即，，        ………………10分

也就是，，

即，即只要　 ………………12分　 

当时，（＊）对任意的s都成立，从而总能被轴平分．

所以在x轴上存在定点，使得总能被轴平分

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网