题目内容
(本小题满分12分)
如图,四边形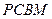 是直角梯形,∠
是直角梯形,∠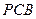 =90°,
=90°,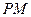 ∥
∥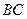 ,
,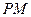 =1,
=1,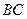 =2,又
=2,又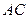 =1,∠
=1,∠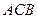 =120°,
=120°, ⊥
⊥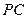 ,直线
,直线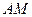 与直线
与直线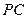 所成的角为60°.
所成的角为60°.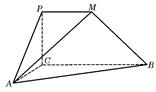
(Ⅰ)求证:平面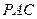 ⊥平面
⊥平面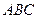 ;
;
(Ⅱ)求二面角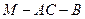 的余弦值.
的余弦值.

证明:(Ⅰ)因为 ,所以
,所以 .
.
又因为 ,
, . …………………………………3分
. …………………………………3分
(Ⅱ)由(I)知, 在面
在面 内的射影
内的射影 必在
必在 上,易知
上,易知 .
.
因为直线 与直线
与直线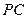 所成的角为
所成的角为 ,所以
,所以 .
.
在 中,由余弦定理得
中,由余弦定理得 .
.
在 中,
中, . …………………………….5分
. …………………………….5分
建立如图所示的空间直角坐标系 .
.
由题意知 ,
, .
.
所以 ,
, .
.
………………………………………….7分
设平面 的一个法向量为
的一个法向量为 ,
,
则 .
.
取
 . …………………………………………………9分
. …………………………………………………9分
又平面 的一个法向量为
的一个法向量为 . ………………………………………….10分
. ………………………………………….10分
设 与
与 所成的角为
所成的角为 ,则
,则 . ……………………..11分
. ……………………..11分
显然,二面角 为锐角,故二面角
为锐角,故二面角 的余弦值为
的余弦值为 .
.
………………………………………………………………………12分
解析

练习册系列答案
相关题目