题目内容
已知函数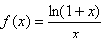 。
。
(1)确定y=f(x)在(0,+∞)上的单调性;
(2)若h(x)=x·f(x)-x-ax3在(0,2)上有极值,求实数a 的取值范围。
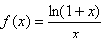 。
。(1)确定y=f(x)在(0,+∞)上的单调性;
(2)若h(x)=x·f(x)-x-ax3在(0,2)上有极值,求实数a 的取值范围。
解:(1)由已知函数求导得
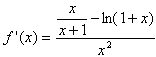
设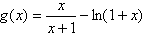
则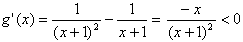
在(0,+∞)上恒成立,
所以g(x)在(0,+∞)上单调递减,所以g(x)<g(0)=0,所以f'(x)<0,
因此f(x)在(0,+∞)上单调递减。
(2)由h(x)=ln(1+x)-x-ax3可得
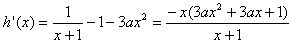
若a≥0,对任意的x∈(0,+∞),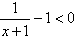 ,
,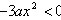
所以h'(x)<0,
所以h(x)在(0,2)上单调递减,
则f(x)在(0,2)上无极值;
若a<0,h(x)=x·f(x)-x-ax3在(0,2)上有极值的充要条件是
φ(x)=3ax2+3ax+1在(0,2)上有零点,
所以φ(0)·φ(2)<0,解得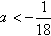
综上,a的取值范围是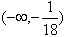 。
。
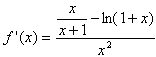
设
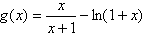
则
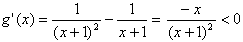
在(0,+∞)上恒成立,
所以g(x)在(0,+∞)上单调递减,所以g(x)<g(0)=0,所以f'(x)<0,
因此f(x)在(0,+∞)上单调递减。
(2)由h(x)=ln(1+x)-x-ax3可得
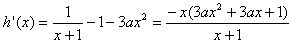
若a≥0,对任意的x∈(0,+∞),
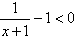 ,
,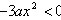
所以h'(x)<0,
所以h(x)在(0,2)上单调递减,
则f(x)在(0,2)上无极值;
若a<0,h(x)=x·f(x)-x-ax3在(0,2)上有极值的充要条件是
φ(x)=3ax2+3ax+1在(0,2)上有零点,
所以φ(0)·φ(2)<0,解得
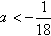
综上,a的取值范围是
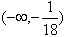 。
。
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
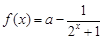 .;
.;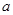 的值,使
的值,使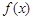 为奇函数;
为奇函数;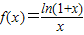 .?
.?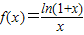 .?
.?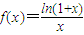 .?
.?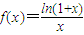 .?
.?