题目内容
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.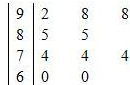
(Ⅰ)计算样本的平均成绩及方差;
(Ⅱ)现从80分以上的样本中随机抽出2名学生,求抽出的2名学生的成绩分别在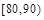 、
、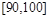 上的概率.
上的概率.
(Ⅰ)80,175;(Ⅱ) .
.
解析试题分析:(Ⅰ)解法思路明确,对计算能力要求较高.
利用样本的平均数计算公式可得; ,
,
应用方差计算公式可得,方差 ;
;
(Ⅱ)观察茎叶图,利用古典概型概率的计算公式,关键是弄清两个事件数.
试题解析:(Ⅰ)样本的平均成绩 , 2分
, 2分
方差


 4分
4分 ; 6分
; 6分
(Ⅱ)从80分以上的样本中随机抽出2名学生,共有10种不同的抽取方法, 8分
而抽出的2名学生的分数分别在 ,
,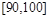 上共有6中不同的抽取方法,因此所求的概率为
上共有6中不同的抽取方法,因此所求的概率为 . 12分
. 12分
考点:茎叶图,平均数、方差,古典概型.

练习册系列答案
相关题目
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
| 组号 | 分组 | 频数 | 频率 |
| 第1组 |  | 5 | 0.050 |
| 第2组 | 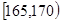 | ① | 0.350 |
| 第3组 |  | 30 | ② |
| 第4组 | 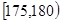 | 20 | 0.200 |
| 第5组 | 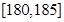 | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
(1)请先求出频率分布表中①、②位置相应的数据,再在答题卷上完成下列频率分布直方图;

(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
某学校100名学生期中考试语文成绩的频率分布直方图如下右图所示,其中成绩分组区间是: ,
,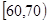 ,
, ,
,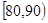 ,
, 。
。
求图中a的值;
根据频率分布直方图,估计这100名学生语文成绩的平均分;
若这100名学生语文成绩某些分数段的人数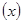 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数
之比如下表所示,求数学成绩在 之外的人数。
之外的人数。
| 分数段 |  | 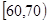 |  | 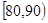 |
x :y :y | 1:1 | 2:1 | 3:4 | 4:5 |
在对某校高一学生体育选修项目的一次调查中,共调查了160人,其中女生85人,男生75人.女生中有60人选修排球,其余的人选修篮球;男生中有20人选修排球,其余的人选修篮球.(每人必须选一项,且只能选一项)
根据以上数据建立一个2×2的列联表;
能否在犯错误的概率不超过0.001的前提下认为性别与体育选修项目有关?
参考公式及数据: ,其中
,其中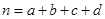 .
.
| K2≥k0 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

 (简称血酒含量,单位是毫克/
(简称血酒含量,单位是毫克/ 毫升),当
毫升),当 时,为“酒后驾车”;当
时,为“酒后驾车”;当 时,为“醉酒驾车”.某市公安局交通管理部门于
时,为“醉酒驾车”.某市公安局交通管理部门于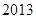 年
年 月的某天晚上
月的某天晚上 点至
点至 名饮酒后违法驾驶机动车者,如图为这
名饮酒后违法驾驶机动车者,如图为这 的人数计入
的人数计入 人数之内).
人数之内).
 人,求
人,求 人为“酒后驾车”另
人为“酒后驾车”另
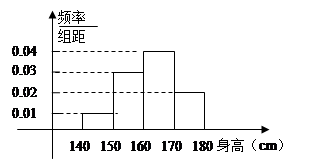
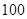 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)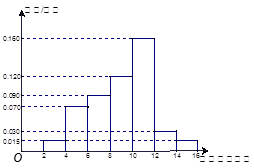
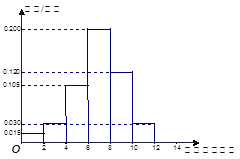
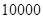 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是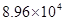 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;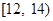 内的家庭中选出
内的家庭中选出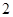 户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率
户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率