题目内容
【题目】已知![]() .
.
(1)若函数![]() 有两个零点,求
有两个零点,求![]() 的取值范围;
的取值范围;
(2)证明:当![]() 时,对任意满足
时,对任意满足![]() 的正实数
的正实数![]() ,
,![]() ,都有
,都有![]() .
.
【答案】(1) (2)证明见解析
(2)证明见解析
【解析】
(1)由![]() 求导得到
求导得到![]() ,再分
,再分![]() 和
和![]() 两种情况结合零点存在定理讨论求解.
两种情况结合零点存在定理讨论求解.
(2)当![]() 时,由
时,由![]() ,得到
,得到 ,然后两式相减解得
,然后两式相减解得 ,
,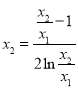 ,令
,令![]() ,则
,则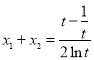 ,然后构造函数
,然后构造函数![]() ,用导数法证明
,用导数法证明![]() 即可.
即可.
(1)![]() 的定义域是
的定义域是![]() ,
,![]() .
.
①当![]() 时,
时,![]() ,
,![]() 在定义域上单调递增,不可能有两个零点;
在定义域上单调递增,不可能有两个零点;
②当![]() 时,由
时,由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在定义域上单调递减;
在定义域上单调递减;
当![]() 时,
时,![]() ,
,![]() 的定义域上单调递增;
的定义域上单调递增;
∴![]() 时,
时,![]() 取得极小值.
取得极小值.
因为![]() 有两个零点,所以
有两个零点,所以![]() ,解得
,解得![]() ,
,
∵![]() ,∴
,∴![]() 在
在![]() 有唯一实数根:
有唯一实数根:
取![]() ,
,
设![]() ,
,![]() ,
,
所以![]() 在
在![]() 上递减,
上递减,
所以![]() ,
,
即![]() ,
,
则![]() ,
,
∴![]() 在
在![]() 有唯一实数根.
有唯一实数根.
综上,![]() 的取值范围是
的取值范围是 .
.
(2)当![]() 时,由
时,由![]() ,得
,得 ,
,
两式相减得:![]() ,
,
则 ,
,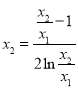 ,
,
令![]() ,则
,则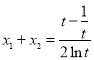 ,
,
设![]() ,
,![]() ,
,
∴![]() 在
在![]() 上为增函数,
上为增函数,![]() ,
,
又![]() ,
,
∴ ,
,
即![]() .
.

练习册系列答案
相关题目
【题目】今年情况特殊,小王在居家自我隔离时对周边的水产养殖产业进行了研究.![]() 、
、![]() 两个投资项目的利润率分别为投资变量
两个投资项目的利润率分别为投资变量![]() 和
和![]() .根据市场分析,
.根据市场分析,![]() 和
和![]() 的分布列分别为:
的分布列分别为:
| 5% | 10% | ||
| 0.8 | 0.2 | ||
| 2% | 8% | 12% | |
| 0.2 | 0.5 | 0.3 | |
(1)若在![]() 两个项目上各投资
两个项目上各投资![]() 万元,
万元,![]() 和
和![]() 分别表示投资项目
分别表示投资项目![]() 和
和![]() 所获得的利润,求方差
所获得的利润,求方差![]() ,
,![]() ;
;
(2)若在![]() 两个项目上共投资
两个项目上共投资![]() 万元,那么如何分配,能使投资
万元,那么如何分配,能使投资![]() 项目所得利润的方差与投资
项目所得利润的方差与投资![]() 项目所得利润的方差的和最小,最小值是多少?
项目所得利润的方差的和最小,最小值是多少?
(注:![]() )
)