题目内容
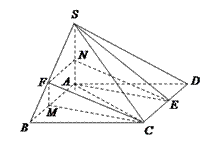
如图,在四棱锥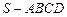 中,
中,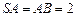 ,
,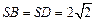 ,底面
,底面 是菱形,且
是菱形,且 ,
,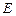 为
为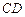 的中点.
的中点.
(1)求四棱锥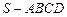 的体积;
的体积;
(2)证明: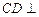 平面
平面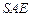 ;
;
(3)侧棱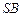 上是否存在点
上是否存在点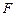 ,使得
,使得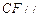 平面
平面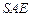 ?并证明你的结论.
?并证明你的结论.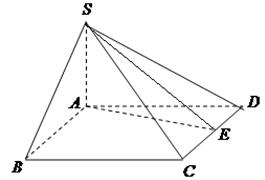
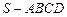 中,
中,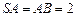 ,
,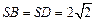 ,底面
,底面 是菱形,且
是菱形,且 ,
,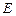 为
为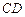 的中点.
的中点.(1)求四棱锥
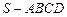 的体积;
的体积;(2)证明:
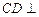 平面
平面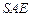 ;
;(3)侧棱
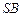 上是否存在点
上是否存在点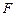 ,使得
,使得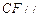 平面
平面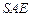 ?并证明你的结论.
?并证明你的结论.
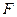 为侧棱
为侧棱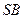 的中点时,
的中点时,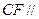 平面
平面
解:(1)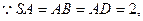
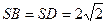 ,
,
则有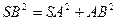 ,
,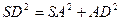 ,
,
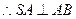 ,
,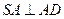 又
又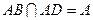
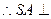 底面
底面 ,………………………(2分)
,………………………(2分)
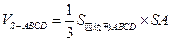
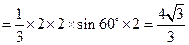 ……………(4分)
……………(4分)
(2)证明: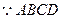 是菱形,
是菱形,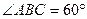 ,
,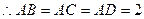 ,
,
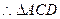 为正三角形, 又
为正三角形, 又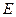 为
为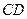 的中点,
的中点,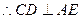 …………………(6分)
…………………(6分)
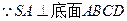
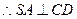
由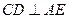 ,
,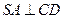 ,
,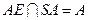 ,
,
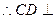 平面
平面 ……………………………………………………(8分)
……………………………………………………(8分)
(3)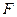 为侧棱
为侧棱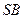 的中点时,
的中点时,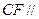 平面
平面 . ……………………………(10分)
. ……………………………(10分)
证法一:设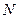 为
为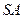 的中点,连
的中点,连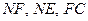 ,则
,则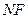 是
是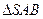 的中位线,
的中位线,
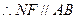 且
且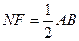 ,又
,又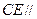 且
且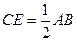 ,
,
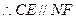 且
且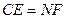 ,
,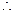 四边形
四边形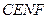 为平行四边形,
为平行四边形,
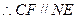 ,
,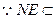 平面
平面 ,
,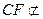 平面
平面 ,
,
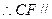 平面
平面 . ………………(12分)
. ………………(12分)
证法二:设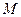 为
为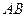 的中点,连
的中点,连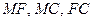 ,则
,则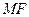 是
是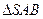 的中位线,
的中位线,
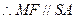 ,
,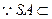 平面
平面 ,
,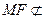 平面
平面 ,
,
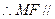 平面
平面 .
.
同理,由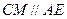 ,得
,得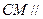 平面
平面 .
.
又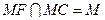 ,
,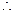 平面
平面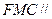 平面
平面 ,
,
又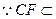 平面
平面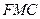 ,
, 平面
平面 . ……………………………(12分)
. ……………………………(12分)
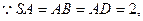
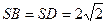 ,
,
则有
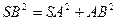 ,
,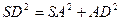 ,
,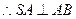 ,
,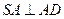 又
又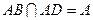
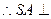 底面
底面 ,………………………(2分)
,………………………(2分)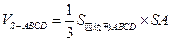
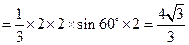 ……………(4分)
……………(4分) (2)证明:
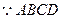 是菱形,
是菱形,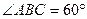 ,
,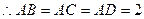 ,
,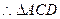 为正三角形, 又
为正三角形, 又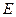 为
为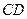 的中点,
的中点,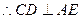 …………………(6分)
…………………(6分)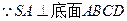
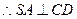
由
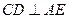 ,
,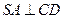 ,
,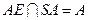 ,
,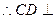 平面
平面 ……………………………………………………(8分)
……………………………………………………(8分)(3)
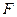 为侧棱
为侧棱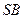 的中点时,
的中点时,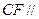 平面
平面 . ……………………………(10分)
. ……………………………(10分)证法一:设
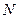 为
为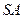 的中点,连
的中点,连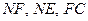 ,则
,则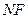 是
是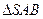 的中位线,
的中位线,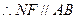 且
且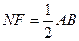 ,又
,又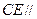 且
且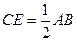 ,
, 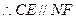 且
且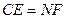 ,
,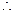 四边形
四边形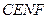 为平行四边形,
为平行四边形, 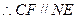 ,
,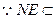 平面
平面 ,
,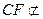 平面
平面 ,
,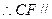 平面
平面 . ………………(12分)
. ………………(12分)证法二:设
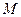 为
为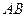 的中点,连
的中点,连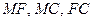 ,则
,则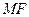 是
是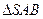 的中位线,
的中位线,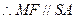 ,
,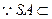 平面
平面 ,
,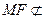 平面
平面 ,
,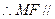 平面
平面 .
. 同理,由
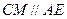 ,得
,得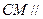 平面
平面 .
.又
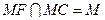 ,
,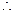 平面
平面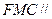 平面
平面 ,
, 又
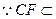 平面
平面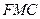 ,
,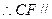 平面
平面 . ……………………………(12分)
. ……………………………(12分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
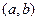 为圆心,以
为圆心,以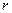 为半径的圆的方程为
为半径的圆的方程为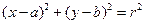 ,类似的在空间以点
,类似的在空间以点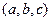 为球心,以
为球心,以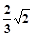
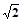
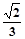
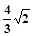
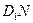 所成的角,则
所成的角,则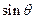 =" " ( )
=" " ( ) 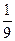
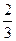
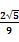
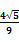
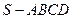 中,
中,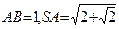 ,则
,则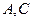 两点间的球面距离为 .
两点间的球面距离为 .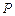 是边长为
是边长为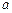 的正
的正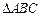 内的一点,
内的一点,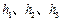 ,则
,则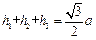 ;类比到空间,设
;类比到空间,设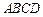 内的一点,则
内的一点,则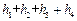 = .
= . BC中,PA⊥平面ABC、△ABC为正三角形,且PA=AB=2,则三棱锥P—ABC的侧视图面积为 。
BC中,PA⊥平面ABC、△ABC为正三角形,且PA=AB=2,则三棱锥P—ABC的侧视图面积为 。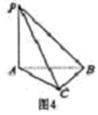
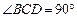 ,BC =" CD" = 1,AB⊥面BCD,
,BC =" CD" = 1,AB⊥面BCD,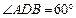 ,点E、F分别在AC、AD上,使面BEF⊥ACD,且EF∥CD,则平面BEF与平面BCD所成的二面角的正弦值为( )
,点E、F分别在AC、AD上,使面BEF⊥ACD,且EF∥CD,则平面BEF与平面BCD所成的二面角的正弦值为( )