Question

已知函数f（x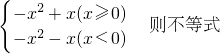）=f（x）+2＞0的解集是

1. A.
   （-2，2）
2. B.
   （-∞，-2）∪（2，+∞）
3. C.
   （-1，1）
4. D.
   （-∞，-1）∪（1，+∞）

Answer 1

A
分析：已知分段函数f（x）求不等式f（x）+2＞0的解集，要分类讨论：①当x≥0时；②当x＜0时，分别代入不等式f（x）+2＞0，从而求出其解集．
解答：①当x≥0时；f（x）=-x²+x，
∵-x²+x+2＞0，
x²-x-2＜0，
解得，-1＜x＜2，
∴0≤x＜2；
②当x＜0时；f（x）=-x²-x，
∴-x²-x+2＞0，
解得，-2＜x＜1，
∴-2＜x＜0，
综上①②知不等式f（x）+2＞0的解集是：（-2，2），
故选A．
点评：此题主要考查一元二次不等式的解法，在解答的过程中运用的分类讨论的思想，是一道比较基础的题目．