题目内容
若数列{an}和{bn}满足关系:an=
,an+1=
(an+
)n∈N*,a1=3.
(1)求证:数列{lgbn}是等比数列;
(2)设Tn=b1b2b3…bn,求满足Tn≥
的n的集合M;
(3)设cn=
,{cn}的前n项和为Sn,试探索an与Sn之间的关系式.
| 1+bn |
| 1-bn |
| 1 |
| 2 |
| 1 |
| an |
(1)求证:数列{lgbn}是等比数列;
(2)设Tn=b1b2b3…bn,求满足Tn≥
| 1 |
| 128 |
(3)设cn=
2
| ||
| bn-1 |
分析:(1)要证数列{lgbn}是等比数列,需找到与lgbn有关的式子,可把an=
代入an+1=
(an+
)转化成与lgbn有关的式子;
(2)求出bn后,代入Tn=b1b2b3…bn,然后运用同底幂相乘底数不变指数相化简得Tn,最后代入Tn≥
求n的集合;
(3)因为an、cn都与bn有关系,把bn代入an、cn的表达式后得出an-an-1=cn(n≥2),累加后得an-a1=sn-c1,从而得到an与Sn之间的关系式.
| 1+bn |
| 1-bn |
| 1 |
| 2 |
| 1 |
| an |
(2)求出bn后,代入Tn=b1b2b3…bn,然后运用同底幂相乘底数不变指数相化简得Tn,最后代入Tn≥
| 1 |
| 128 |
(3)因为an、cn都与bn有关系,把bn代入an、cn的表达式后得出an-an-1=cn(n≥2),累加后得an-a1=sn-c1,从而得到an与Sn之间的关系式.
解答:解:(1)∵an=
∴an+1=
由an+1=
(an+
),得
=
(
+
)=
,
∴bn+1=
,即lgbn+1=2lgbn,
又
=a1=3,b1=
,lgb1=-lg2≠0,
所以数列{lgbn}是等比数列,首项-lg2,公比2;
(2)由(1)得:lgbn=(-lg2)•2n-1⇒bn=(
)2n-1,Tn=b1b2…bn=(
)1+2+…+2n-1=(
)2n-1≥
⇒2n-1≤7
∴2n≤8,即n≤3,又因为n∈N*
∴M={1,2,3};
(3)因为an=
,所以an=
=
=1+
=1+
-
同理an-1═
=1+
,则an-an-1=
,又cn=
=
∴an-an-1=cn(n≥2),
∴an-a1=sn-c1,
∵a1=3,c1=-2
∴an=Sn+3+2
.
| 1+bn |
| 1-bn |
| 1+bn+1 |
| 1-bn-1 |
| 1 |
| 2 |
| 1 |
| an |
| 1+bn+1 |
| 1-bn+1 |
| 1 |
| 2 |
| 1+bn |
| 1-bn |
| 1-bn |
| 1+bn |
1+
| ||
1-
|
∴bn+1=
| b | 2 n |
又
| 1+b1 |
| 1-b1 |
| 1 |
| 2 |
所以数列{lgbn}是等比数列,首项-lg2,公比2;
(2)由(1)得:lgbn=(-lg2)•2n-1⇒bn=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 128 |
∴2n≤8,即n≤3,又因为n∈N*
∴M={1,2,3};
(3)因为an=
| 1+bn |
| 1-bn |
1+(
| ||
1-(
|
| 22n-1+1 |
| 22n-1-1 |
| 2 |
| (22n-2+1)(22n-2-1) |
| 1 |
| 22n-2-1 |
| 1 |
| 22n-2+1 |
同理an-1═
| 22n-2+1 |
| 22n-2-1 |
| 2 |
| 22n-2-1 |
| 2•22n-2 |
| 1-22n-1 |
2
| ||
| 1-bn |
| 2•22n-2 |
| 1-22n-1 |
∴an-an-1=cn(n≥2),
∴an-a1=sn-c1,
∵a1=3,c1=-2
| 2 |
∴an=Sn+3+2
| 2 |
点评:本题考查了数列求和与不等式的综合,试题中以bn为媒介,联系了两个数列an与cn,最后考查了数列求和的累加法.解答该题的关键是如何顺利的把数列bn的通项转化成an与bn的表达式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
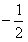 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;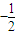 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;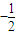 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;