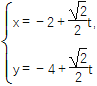题目内容
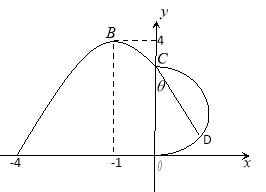
【题目】如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数![]() ,
,![]() 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.
(1)试确定A,![]() 和
和![]() 的值;
的值;
(2)现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设![]() (弧度),试用
(弧度),试用![]() 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
【答案】(1)![]() ;(2)造价
;(2)造价![]() ,
,![]() ,
,![]() 在
在![]() 时取极大值,也即造价预算最大值为(
时取极大值,也即造价预算最大值为(![]() )万元.
)万元.
【解析】
试题分析:(1)由“五点法”可求得![]() ;(2)由(1)求出
;(2)由(1)求出![]() 点坐标,得半圆的半径,用
点坐标,得半圆的半径,用![]() 表示出弦长
表示出弦长![]() 和弧长
和弧长![]() ,由题意可得造价
,由题意可得造价![]() ,
,![]() ,下面用导数的知识求出
,下面用导数的知识求出![]() 的最大值.
的最大值.
试题解析:(1)因为最高点B(-1,4),所以A=4;
![]() ,
,
因为![]()
代入点B(-1,4),
![]() ,
,
又![]() ;
;
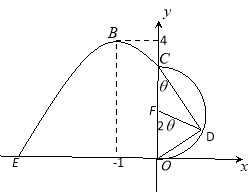
(2)由(1)可知:
![]() ,得点C
,得点C![]() 即
即![]() ,
,
取CO中点F,连结DF,因为弧CD为半圆弧,所以![]() ,
,
即![]() ,则圆弧段
,则圆弧段![]() 造价预算为
造价预算为![]() 万元,
万元,
![]() 中,
中,![]() ,则直线段CD造价预算为
,则直线段CD造价预算为![]() 万元
万元
所以步行道造价预算![]() ,
,![]() .
.
由![]() 得当
得当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递减
上单调递减
所以![]() 在
在![]() 时取极大值,也即造价预算最大值为(
时取极大值,也即造价预算最大值为(![]() )万元.……16分
)万元.……16分

【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
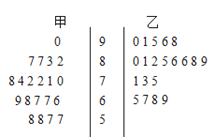
(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀,请填写![]() 列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式与临界值表: 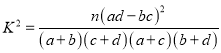 .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |