题目内容
已知函数f(x)=x3 + x2,数列|x![]() |(x
|(x![]() >0)的第一项x
>0)的第一项x![]() =1,以后各项按如下方式取定:曲线x=f(x)在
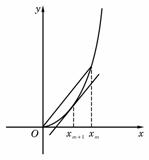
=1,以后各项按如下方式取定:曲线x=f(x)在![]() 处的切线与经过(0,0)和(x
处的切线与经过(0,0)和(x![]() ,f (x
,f (x![]() ))两点的直线平行(如图)
))两点的直线平行(如图)
 求证:当
求证:当![]() 时,
时,
(Ⅰ)![]() ;
;
(Ⅱ)![]()
证明:(I)因为![]()
所以曲线![]() 在
在![]() 处的切线斜率
处的切线斜率![]()
因为过(0,0)和![]() 两点的直线斜率是
两点的直线斜率是![]() ,
,
所以![]() .
.
(II)因为函数![]() 当
当![]() 时单调递增,
时单调递增,
而![]()
![]()
![]()
所以![]() ,即
,即![]() ,
,
因此![]()
又因为![]()
令![]()
则![]()
因为![]()
所以![]()
因此![]()
故![]()

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目