题目内容
数列{an}中,a1=1,当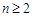 时,其前n项和满足
时,其前n项和满足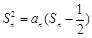 .
.
(Ⅰ)求Sn的表达式;
(Ⅱ)设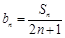 ,数列{bn}的前n项和为
,数列{bn}的前n项和为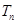 ,求
,求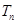 .
.
【答案】
(Ⅰ)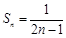 ;(Ⅱ)
;(Ⅱ)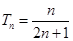 .
.
【解析】
试题分析:(Ⅰ)求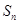 的表达式,数列{an}中,a1
= 1,当
的表达式,数列{an}中,a1
= 1,当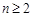 时,其前n项和满足
时,其前n项和满足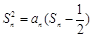 ,由
,由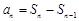 代换
代换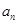 得,
得,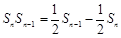 ,两边同除以
,两边同除以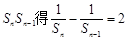 ,得数列
,得数列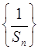 ,是等差数列,从而可求数列
,是等差数列,从而可求数列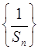 的通项公式,从而得
的通项公式,从而得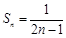 ;(Ⅱ)设
;(Ⅱ)设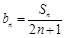 ,数列{bn}的前n项和为
,数列{bn}的前n项和为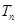 ,求
,求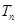 ,首先求数列{bn}的通项公式,
,首先求数列{bn}的通项公式,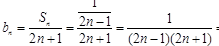 ,显然利用拆项相消法求数列的前n项和.
,显然利用拆项相消法求数列的前n项和.
试题解析:(Ⅰ)当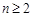 时,
时,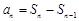 代入已知得
代入已知得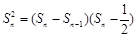
化简得: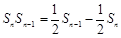 , 两边同除以
, 两边同除以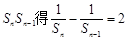
∴ 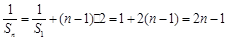
∴ 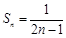 ,当
,当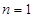 时,也成立
时,也成立
(Ⅱ)∵ 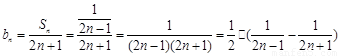
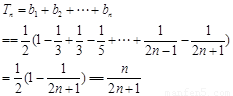
考点: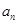 与
与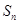 的关系,等差数列的判断及求通项公式,数列求和.
的关系,等差数列的判断及求通项公式,数列求和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}中,a1=
,an+an+1=
,n∈N*,则
(a1+a2+…+an)等于( )
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|