题目内容
(2013•临沂一模)直线y=x的任意点P与圆x2+y2-10x-2y+24=0的任意点Q间距离的最小值为
.
| 2 |
| 2 |
分析:先求圆心(5,1)到直线x-y=0的距离d,结合圆的性质可知d-r即为所求PQ最小距离.
解答:解:圆x2+y2-10x-2y+24=0的圆心(5,1),r=
而圆心到直线x-y=0的距离d=
=2
故圆x2+y210x-2y+24=0上的动点P到直线x-y=0的距离的最小值为 2
-
=
,
故答案为:
| 2 |
而圆心到直线x-y=0的距离d=
| |5-1| | ||
|
| 2 |
故圆x2+y210x-2y+24=0上的动点P到直线x-y=0的距离的最小值为 2
| 2 |
| 2 |
| 2 |
故答案为:
| 2 |
点评:本题考查直线和圆的位置关系,点到直线的距离公式,求出圆心到直线x-y=0的距离,是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
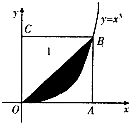 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )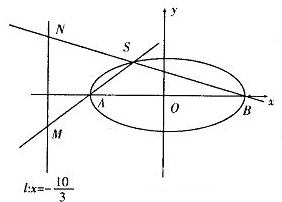 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: