Question

设f(x)＝aln x＋＋x＋1，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线垂直于y轴．

(1)求a的值；

(2)求函数f(x)的极值．

Answer 1

(1)因f(x)＝aln x＋＋x＋1.

故f′(x)＝－＋.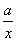

由于曲线y＝f(x)在点(1，f(1))处的切线垂直于y轴，故该切线斜率为0，即f′(1)＝0，从而a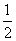－＋＝0，

解得a＝－1.

(2)由(1)知f(x)＝－ln x＋＋x＋1(x>0)，

当x∈(0,1)时，f′(x)<0，故f(x)在(0,1)上为减函数；

当x∈(1，＋∞)时，f′(x)>0，故f(x)在(1，＋∞)上为增函数．

故f(x)在x＝1处取得极小值f(1)＝3.