题目内容
已知等腰直角三角形ABC，沿其斜边AB边上的高CD对折，使△ACD与△BCD所在平面垂直，此时，∠ACB= ．
分析：先判断折叠后△ACD，△BCD，△ABD的形状，进而判断出△ABC的形状，从而可得答案．
解答：解：如图所示：
折叠后∠ACD=∠BCD=45°，AD⊥CD，BD⊥CD，
∴∠ADB为二面角A-CD-B的平面角，
又平面ACD⊥平面BCD，
∴∠ADB=90°，
∴△ADB为等腰直角三角形，
设AD=1，则AC=BC=AB=
，
∴△ABC为正三角形，
∴∠ACB=60°．
故答案是60°
折叠后∠ACD=∠BCD=45°，AD⊥CD，BD⊥CD，
∴∠ADB为二面角A-CD-B的平面角，
又平面ACD⊥平面BCD，
∴∠ADB=90°，
∴△ADB为等腰直角三角形，
设AD=1，则AC=BC=AB=
| 2 |
∴△ABC为正三角形，
∴∠ACB=60°．
故答案是60°
点评：本题考查的是翻折变换的性质，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等的知识是解答此题的关键．
练习册系列答案
相关题目
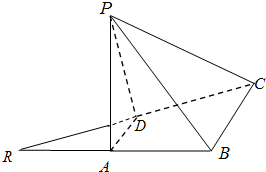如图，已知等腰直角三角形RBC，其中∠RBC=90°，RB=BC=2．点A、D分别是RB、RC的中点，现将△RAD沿着边AD折起到△PAD位置，使PA⊥AB，连接PB、PC．
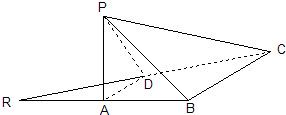如图，已知等腰直角三角形RBC，其中∠RBC=90°，RB=BC=2．点A、D分别是RB、RC的中点，现将△RAD沿着边AD折起到△PAD位置，使PA⊥AB，连接PB、PC．