题目内容
已知a,b,c是△ABC三边长且a2+b2-c2=ab,△ABC的面积S=10
,c=7.
(Ⅰ)求角C;
(Ⅱ)求a,b的值.
| 3 |
(Ⅰ)求角C;
(Ⅱ)求a,b的值.
(Ⅰ)∵a2+b2-c2=ab,
∴cosC=
=
,
∵0°<C<180°,
∴C=60°;
(Ⅱ)∵△ABC的面积S=10
,
∴
absinC=10
,
∴ab=40①,
∵c2=a2+b2-ab=(a+b)2-3ab=49,
∴a+b=13②,
由①②,解得a=8,b=5或a=5,b=8.
∴cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∵0°<C<180°,
∴C=60°;
(Ⅱ)∵△ABC的面积S=10
| 3 |
∴
| 1 |
| 2 |
| 3 |
∴ab=40①,
∵c2=a2+b2-ab=(a+b)2-3ab=49,
∴a+b=13②,
由①②,解得a=8,b=5或a=5,b=8.

练习册系列答案
相关题目

 中,
中, ,
,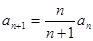 ,则
,则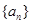 满足
满足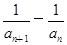 =
=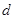 (n∈N*,
(n∈N*,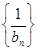 为“调和数列”,且
为“调和数列”,且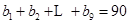 ,则
,则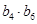 的最大值是 ( )
的最大值是 ( )