Question

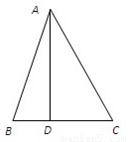
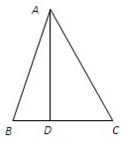如图，在锐角△ABC中，AD⊥BC，垂足为D，且BD：DC：AD=2：3：6，则∠BAC的大小为

 

．

Answer 1

分析：先令∠BAD=α，∠CAD=β，则∠BAC=α+β，然后分别在Rt△ABD和Rt△ADC中，利用tanα=

BD

AD

和tanβ=

CD

AD

求得tanα和tanβ的值，然后利用正切的两角和公式求得tan（α+β）的值，进而求得α+β即∠BAC．

解答：解：令∠BAD=α，∠CAD=β，则∠BAC=α+β
tanα=

BD

AD

=

1

3

tanβ=

CD

AD

=

3

6

=

1

2

∴tan（α+β）=

tanα+tanβ

1-tanαtanβ

=

1 2 + 1 3

1- 1 2 × 1 3

=1
又0＜∠BAC＜π，则0＜α+β＜π
所以α+β=

π

4

即∠BAC=

π

4

故答案为：

π

4

点评：本题主要考查了解三角形，正切的两角和公式化简求值．在解三角形问题中求角的值，一般是通过求角的三角函数值来求．