题目内容
 【几何证明选讲选做题】
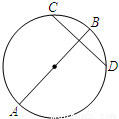
【几何证明选讲选做题】如图,P是⊙O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4
| 3 |
分析:连接OD,首先根据切割线定理计算出PE的长,再进一步计算出OP的长和圆的半径的长;从而在直角三角形OPD中,计算要求的角.
解答: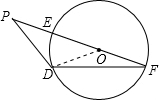 解:连接DO;
解:连接DO;
∵PD为切线,PEF为割线,由切割线定理
PD2=PE•PF;
∵PD=4
,PF=12,
∴PE=4,
∴EF=PF-PE=8,EO=4;
∵PD为切线,D为切点,
∴OD⊥PD;
∵在Rt△PDO中,OD=4,PD=4
,
∴∠DPO=30°.
 解:连接DO;
解:连接DO;∵PD为切线,PEF为割线,由切割线定理
PD2=PE•PF;
∵PD=4
| 3 |
∴PE=4,
∴EF=PF-PE=8,EO=4;
∵PD为切线,D为切点,
∴OD⊥PD;
∵在Rt△PDO中,OD=4,PD=4
| 3 |
∴∠DPO=30°.
点评:此题综合运用了切割线定理、切线的性质定理以及直角三角形的性质和圆周角定理.

练习册系列答案
相关题目
 【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤. ,求线段AC的长度.
,求线段AC的长度. 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程. (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
 ,求线段AC的长度.
,求线段AC的长度. 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程. (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
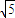 ,求线段AC的长度.
,求线段AC的长度. 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.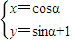 (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.