题目内容
在△ABC中,a,b,c分别是内角A,B,C所对的边,若ccosA=b,则△ABC形状为( )A.一定是锐角三角形
B.一定是钝角三角形
C.一定是直角三角形
D.可能是锐角三角形,也可能是钝角三角形
【答案】分析:利用正弦定理及和角的正弦公式化简,结合角A,C是△ABC的内角,即可得到结论.
解答:解:∵ccosA=b
∴sinCcosA=sinB=sin(A+C)
∴sinCcosA=sinAcosC+cosAsinC
∴sinAcosC=0
∵角A,C是△ABC的内角
∴cosC=0
∴C=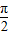
∴△ABC形状为直角三角形
故选C.
点评:本题考查正弦定理的运用,考查学生的运算能力,属于基础题.
解答:解:∵ccosA=b
∴sinCcosA=sinB=sin(A+C)
∴sinCcosA=sinAcosC+cosAsinC
∴sinAcosC=0
∵角A,C是△ABC的内角
∴cosC=0
∴C=
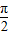
∴△ABC形状为直角三角形
故选C.
点评:本题考查正弦定理的运用,考查学生的运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|