题目内容
设函数f(x)=ex+x-2,g(x)=lnx+x2-3,若实数a,b满足f(a)=0,g(b)=0,则( )
| A、0<g(a)<f(b) | B、f(b)<g(a)<0 | C、f(b)<0<g(a) | D、g(a)<0<f(b) |
分析:先判断函数f(x),g(x)在R上的单调性,再利用f(a)=0,g(b)=0判断a,b的取值范围,即可得到正确答案.
解答:解:∵y=ex和y=x-2是关于x的单调递增函数,
∴函数f(x)=ex+x-2在R上单调递增,
分别作出y=ex,y=2-x的图象如右图所示,
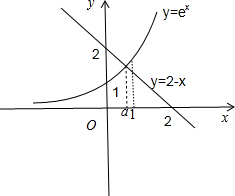 ∴f(0)=1+0-2<0,f(1)=e-1>0,
∴f(0)=1+0-2<0,f(1)=e-1>0,
又∵f(a)=0,
∴0<a<1,
同理,g(x)=lnx+x2-3在R+上单调递增,g(1)=ln1+1-3=-2<0,g(
)=ln
+(
)2-3=
ln3>0,
又∵g(b)=0,
∴1<b<
,
∴g(a)=lna+a2-3<g(1)=ln1+1-3=-2<0,
f(b)=eb+b-2>f(1)=e+1-2=e-1>0,
∴g(a)<0<f(b).
故选:D.
∴函数f(x)=ex+x-2在R上单调递增,
分别作出y=ex,y=2-x的图象如右图所示,
 ∴f(0)=1+0-2<0,f(1)=e-1>0,
∴f(0)=1+0-2<0,f(1)=e-1>0,又∵f(a)=0,
∴0<a<1,
同理,g(x)=lnx+x2-3在R+上单调递增,g(1)=ln1+1-3=-2<0,g(
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
又∵g(b)=0,
∴1<b<
| 3 |
∴g(a)=lna+a2-3<g(1)=ln1+1-3=-2<0,
f(b)=eb+b-2>f(1)=e+1-2=e-1>0,
∴g(a)<0<f(b).
故选:D.
点评:本题考查了函数的性质,考查了函数图象.熟练掌握函数的单调性、函数零点的判定定理是解题的关键.本题运用了数形结合的数学思想方法.属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目