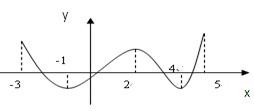
题目内容
函数 的单调递增区间是
的单调递增区间是
- A.(-3,3)
- B.(-3,+∞)
- C.x2+2x+a>0,x∈[1,+∞)
- D.(-∞,-3),(3,+∞)
D
分析:求出函数y的导函数y′,因为要求单调递增区间,令y′>0得到不等式求出x的范围即可.
解答:
∴令y′>0,得:
x<-3),或x>3,
∴函数 的单调递增区间是(-∞,-3),(3,+∞)
的单调递增区间是(-∞,-3),(3,+∞)
故选D.
点评:考查学生掌握利用导数研究函数的单调性的能力.求单调递增区间的方法:先确定函数的定义域然后求出函数的导涵数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数的单调区间,
分析:求出函数y的导函数y′,因为要求单调递增区间,令y′>0得到不等式求出x的范围即可.
解答:

∴令y′>0,得:
x<-3),或x>3,
∴函数
 的单调递增区间是(-∞,-3),(3,+∞)
的单调递增区间是(-∞,-3),(3,+∞)故选D.
点评:考查学生掌握利用导数研究函数的单调性的能力.求单调递增区间的方法:先确定函数的定义域然后求出函数的导涵数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数的单调区间,

练习册系列答案
相关题目