题目内容
(本小题满分12分)
如图,已知正三棱柱![]() -
-![]() 的底面边长为2,侧棱长为
的底面边长为2,侧棱长为![]() ,点E在侧棱
,点E在侧棱![]() 上,点F在侧棱
上,点F在侧棱![]() 上,且
上,且![]() ,.
,.
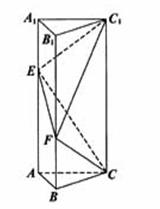 (I) 求证:
(I) 求证:![]() ;
;
(II) 求二面角![]() 的大小。
的大小。
本小题主要考查空间直线与平面的位置关系和二面角的求法,同时考查空间想象能力和推理论证能力。(满分12分)
解法1:(Ⅰ)由已知可得![]()
![]()
于是有![]()
所以![]()
又![]()
由![]()
(Ⅱ)在![]() 中,由(Ⅰ)可得
中,由(Ⅰ)可得![]()
于是有EF2+CF2=CE2,所以![]()
又由(Ⅰ)知CF ![]() C1E,且
C1E,且![]() ,所以CF
,所以CF ![]() 平面C1EF,
平面C1EF,
又![]() 平面C1EF,故CF
平面C1EF,故CF ![]() C1F。
C1F。
于是![]() 即为二面角E—CF—C1的平面角。
即为二面角E—CF—C1的平面角。
由(Ⅰ)知![]() 是等腰直角三角形,所以
是等腰直角三角形,所以![]() ,即所求二面角E—CF—C1的大小为
,即所求二面角E—CF—C1的大小为![]() 。
。
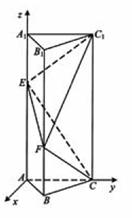
解法2:建立如图所示的空间直角坐标系,则由已知可得
![]()
(Ⅰ)![]()
![]()
![]()
(Ⅱ)![]() ,设平面CEF的一个法向量为
,设平面CEF的一个法向量为![]()
由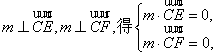
即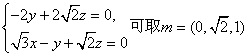
设侧面BC1的一个法向量为![]()
![]()
设二面角E—CF—C1的大小为θ,于是由θ为锐角可得
![]() ,所以
,所以![]()
即所求二面角E—CF—C1的大小为![]() 。
。

练习册系列答案
相关题目