题目内容
若点P是椭圆
上的动点，定点A的坐标为（2，0），则|PA|的取值范围是________．
[
，5]
分析：设出点P的坐标，求出|PA|，利用椭圆的方程，转化为二次函数，利用配方法，即可求得结论．
解答：设P（x，y），则|PA|2=（x-2）2+（y-0）2=x2-4x+4+y2
又∵（x，y）满足
∴|PA|2=x2-4x+4+y2=x2-4x+4+（1-
）=
x2-4x+5其中-3≤x≤3
关于x的二次函数，开口向上，它的对称轴是x=
根据二次函数的性质，可知：
当x=时，|PA|2取得最小值
；当x=-3时，|PA|2取得最大值25．
所以，|PA|的取值范围是[，5]
故答案为：[，5]
点评：本题考查椭圆的标准方程，考查距离的计算，解题的关键是转化为二次函数，利用配方法求解．
，5]分析：设出点P的坐标，求出|PA|，利用椭圆的方程，转化为二次函数，利用配方法，即可求得结论．
解答：设P（x，y），则|PA|2=（x-2）2+（y-0）2=x2-4x+4+y2
又∵（x，y）满足
∴|PA|2=x2-4x+4+y2=x2-4x+4+（1-
）=x2-4x+5其中-3≤x≤3关于x的二次函数，开口向上，它的对称轴是x=
根据二次函数的性质，可知：
当x=
时，|PA|2取得最小值；当x=-3时，|PA|2取得最大值25．所以，|PA|的取值范围是[
，5]故答案为：[
，5]点评：本题考查椭圆的标准方程，考查距离的计算，解题的关键是转化为二次函数，利用配方法求解．
练习册系列答案
相关题目
上的动点， F1，F2为椭圆的两个焦点，O是坐标原点，若M是
F1PF2平分线上的一点，且F1M
MP，则OM的取值范围是__________________。
上的动点，F1，F2为椭圆的两个焦点，O是坐标原点，若M是∠F1PF2的角平分线上一点，且
，则|OM|的取值范围是（ ）
]
）
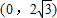
上的动点，定点A的坐标为（2，0），则|PA|的取值范围是 ．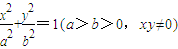
上的动点，F1（-c，0）、F2（c，0）为椭圆的左、右焦点，O为坐标原点，若M是∠F1PF2的角平分线上的一点，且F1M⊥MP，则|OM|的取值范围是（ ）