题目内容
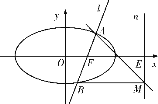
【题目】已知抛物线
的准线l经过椭圆
的左焦点，且l与椭圆交于A，B两点，过椭圆N右焦点
的直线交抛物线M于C，D两点，交椭圆于G，H两点，且
面积为3.
（1）求椭圆N的方程；
（2）当
时，求
.
【答案】（1）
（2）
【解析】
（1）由抛物线方程得出椭圆的左右焦点，
是椭圆的通径长为
，由面积可得
，再由
可求得
得椭圆方程；
（2）设
，
，
，
，M焦点
，设直线为
，代入抛物线方程得
，由抛物线的焦点弦长可求得
，得直线方程，把直线方程代入椭圆方程，由韦达定理得
，由弦长公式
可得弦长，
（1）由抛物线方程得准线方程
，
因为
，
因为抛物线的准线经过椭圆的左焦点，所以，
由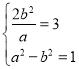
，解得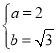
，
所以椭圆方程为；
（2）设，，，，M焦点，设直线为
联立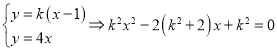
，
当
时，直线为
，
，
，
，
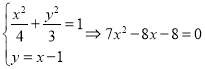当
时，根据对称性，
综上：．.
练习册系列答案
阅读快车系列答案
相关题目
