题目内容
某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为![]() ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为![]()
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为![]() ,求
,求![]() 的分布列与均值E
的分布列与均值E![]() .
.
(I)![]() (II)
(II)![]() (III)分布列见解析,均值为
(III)分布列见解析,均值为![]()
解析:
(I)设徒弟加工1个零件是精品的概率为p1,
则![]()
所以徒弟加工2个零件都是精品的概率是![]() …………3分
…………3分
(II)设徒弟加工零件的精品数多于师父的概率为p,
由(I)知,![]()
师父加工两个零件中,精品个数的分布列如下:
|
| 0 | 1 | 2 |
| P |
|
|
|
徒弟加工两个零件中,精品个数的分布列如下:
|
| 0 | 1 | 2 |
| P |
|
|
|
所以![]() …………9分
…………9分
(III)![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
…………13分
![]() 的期望为
的期望为![]() …………14分
…………14分

练习册系列答案
相关题目
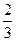 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为
 ,求
,求 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为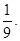 (I)求徒弟加工2个零件都是精品的概率;
(I)求徒弟加工2个零件都是精品的概率; ,求
,求