题目内容
已知函数f(x)=2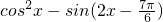 .
.
(Ⅰ)求函数f(x)的最大值,并写出f(x)取最大值时x的取值集合;
(Ⅱ)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(A)= b+c=2,求实数a的最小值.
b+c=2,求实数a的最小值.
解:(Ⅰ)函数f(x)=2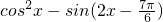 =(1+cos2x)-(sin2xcos
=(1+cos2x)-(sin2xcos -cos2xsin
-cos2xsin )
)
=1+ sin2x+
sin2x+ =1+sin(2x+
=1+sin(2x+ ).
).
∴函数f(x)的最大值为2.
要使f(x)取最大值,则sin(2x+ )=1,∴2x+
)=1,∴2x+ =2kπ+
=2kπ+ (k∈Z)
(k∈Z)
∴x=kπ+ (k∈Z).
(k∈Z).
故x的取值集合为{x|x=kπ+ (k∈Z)}.
(k∈Z)}.
(Ⅱ)由题意,f(A)=sin(2A+ )+1=
)+1= ,化简得sin(2A+
,化简得sin(2A+ )=
)= ,
,
∵A∈(0,π),∴2A+ ∈
∈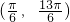 ,∴2A+
,∴2A+ =
= ,∴A=
,∴A=
在△ABC中,根据余弦定理,得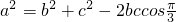 =(b+c)2-3bc.
=(b+c)2-3bc.
由b+c=2,知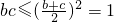 ,即a2≥1.
,即a2≥1.
∴当b=c=1时,实数a取最小值1.
分析:(Ⅰ)利用二倍角公式及辅助角公式,化简函数,即可求得函数的最大值,从而可得f(x)取最大值时x的取值集合;
(Ⅱ)利用f(A)=sin(2A+ )+1=
)+1= ,求得A,在△ABC中,根据余弦定理,利用b+c=2,及
,求得A,在△ABC中,根据余弦定理,利用b+c=2,及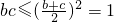 ,即可求得实数a的最小值.
,即可求得实数a的最小值.
点评:本题考查三角函数的化简,考查函数的最值,考查余弦定理的运用,考查基本不等式,综合性强.
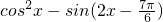 =(1+cos2x)-(sin2xcos
=(1+cos2x)-(sin2xcos -cos2xsin
-cos2xsin )
)=1+
 sin2x+
sin2x+ =1+sin(2x+
=1+sin(2x+ ).
).∴函数f(x)的最大值为2.
要使f(x)取最大值,则sin(2x+
 )=1,∴2x+
)=1,∴2x+ =2kπ+
=2kπ+ (k∈Z)
(k∈Z)∴x=kπ+
 (k∈Z).
(k∈Z).故x的取值集合为{x|x=kπ+
 (k∈Z)}.
(k∈Z)}.(Ⅱ)由题意,f(A)=sin(2A+
 )+1=
)+1= ,化简得sin(2A+
,化简得sin(2A+ )=
)= ,
,∵A∈(0,π),∴2A+
 ∈
∈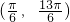 ,∴2A+
,∴2A+ =
= ,∴A=
,∴A=
在△ABC中,根据余弦定理,得
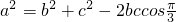 =(b+c)2-3bc.
=(b+c)2-3bc.由b+c=2,知
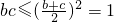 ,即a2≥1.
,即a2≥1.∴当b=c=1时,实数a取最小值1.
分析:(Ⅰ)利用二倍角公式及辅助角公式,化简函数,即可求得函数的最大值,从而可得f(x)取最大值时x的取值集合;
(Ⅱ)利用f(A)=sin(2A+
 )+1=
)+1= ,求得A,在△ABC中,根据余弦定理,利用b+c=2,及
,求得A,在△ABC中,根据余弦定理,利用b+c=2,及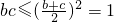 ,即可求得实数a的最小值.
,即可求得实数a的最小值.点评:本题考查三角函数的化简,考查函数的最值,考查余弦定理的运用,考查基本不等式,综合性强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目