题目内容
若不等式ax2+bx+1≥0的解集是{x|- ≤x≤2},求不等式x2+bx+a<0的解集.
≤x≤2},求不等式x2+bx+a<0的解集.
【答案】分析:根据题目给出的不等式ax2+bx+1≥0的解集是{x|- ≤x≤2},得到方程ax2+bx+1=0的两根为-
≤x≤2},得到方程ax2+bx+1=0的两根为- 和2,运用根与系数关系列方程组求出a、b的值,代入要求解的不等式后直接求解.
和2,运用根与系数关系列方程组求出a、b的值,代入要求解的不等式后直接求解.
解答:解:由ax2+bx+1≥0的解集为{x|- ≤x≤2},知a<0,
≤x≤2},知a<0,
又- ,2为方程ax2+bx+1=0的两个根,
,2为方程ax2+bx+1=0的两个根,
∴-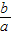 =
= ,即
,即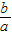 =-
=- .
.
又∵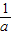 =-
=- ,∴.a=
,∴.a=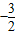 ,b=
,b=
∴不等式x2+bx+a<0变为x2+ x
x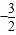 <0,
<0,
即2x2+5x-3<0.
∴所求不等式的解集为{x|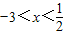 }.
}.
点评:本题考查了一元二次不等式的解法,考查了一元二次不等式的解集与二次不等式所对应的方程根的关系,训练了一元二次方程的根与系数关系,是综合题.
 ≤x≤2},得到方程ax2+bx+1=0的两根为-
≤x≤2},得到方程ax2+bx+1=0的两根为- 和2,运用根与系数关系列方程组求出a、b的值,代入要求解的不等式后直接求解.
和2,运用根与系数关系列方程组求出a、b的值,代入要求解的不等式后直接求解.解答:解:由ax2+bx+1≥0的解集为{x|-
 ≤x≤2},知a<0,
≤x≤2},知a<0,又-
 ,2为方程ax2+bx+1=0的两个根,
,2为方程ax2+bx+1=0的两个根,∴-
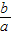 =
= ,即
,即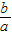 =-
=- .
.又∵
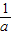 =-
=- ,∴.a=
,∴.a=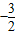 ,b=
,b=
∴不等式x2+bx+a<0变为x2+
 x
x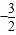 <0,
<0,即2x2+5x-3<0.
∴所求不等式的解集为{x|
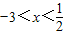 }.
}.点评:本题考查了一元二次不等式的解法,考查了一元二次不等式的解集与二次不等式所对应的方程根的关系,训练了一元二次方程的根与系数关系,是综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目