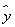Question

若给定一组数据为x_i（i=1，2，…，n），其方差为s²，则数据ax_i（i=1，2，…，n）的方差为

a²S²

．

Answer 1

分析：直接根据方差公式推导结果．

解答：解：设数据为x_i（i=1，2，…，n）的平均数为

.

x

，则数据ax_i（i=1，2，…，n）的平均数为a

.

x

，
根据方差公式，可得s²=

1

n

[(x1-

.

x

)2+(x2-

.

x

)2+…+(xi-

.

x

)2]，
所以数据ax_i（i=1，2，…，n）的方差为

1

n

[(ax1-a

.

x

)2+(ax2-a

.

x

)2+…+(axi-a

.

x

)2]
=

1

n

×a²×[(x1-

.

x

)2+(x2-

.

x

)2+…+(xi-

.

x

)2]
=a²S²
故答案为：a²S²

点评：本题考查方差公式的计算和性质，属于基础题．