题目内容
已知函数:
(1)判定f(x)的奇偶性,并证明;
(2)当x>0时,判断f(x)在(0,2)和(2,+∞)上的单调性,并证明.
【答案】分析:(1)先确定函数的定义域,再利用奇函数的定义,证明函数f(x)=-f(-x),从而函数为奇函数;
(2)利用函数单调性的定义,设任意的x1,x2∈(0,2),当x1<x2时,利用作差法证明f(x1)-f(x2)>0,从而函数f(x)在(0,2)上为减函数,同理可证f(x)在(2,+∞)上为增函数
解答:解:(1)f(x)是奇函数,
因为对于任意的x(x≠0),

所以f(x)是奇函数
(2)①当x>0时,f(x)的单调减区间为(0,2),
对于任意的x1,x2∈(0,2),当x1<x2时
 .
.
因为0<x1x2<4,所以f(x1)-f(x2)>0
所以f(x)在(0,2)上为减函数
②当x>0时,f(x)的单调增区间为(2,+∞),
对于任意的x1,x2∈(2,+∞),当x1<x2时

因为x1x2>4,所以f(x1)-f(x2)<0
所以f(x)在(2,+∞)上为增函数
点评:本题主要考查了证明函数奇偶性的方法,利用函数单调性的定义证明函数单调性的方法步骤,代数变形能力和逻辑推理能力
(2)利用函数单调性的定义,设任意的x1,x2∈(0,2),当x1<x2时,利用作差法证明f(x1)-f(x2)>0,从而函数f(x)在(0,2)上为减函数,同理可证f(x)在(2,+∞)上为增函数
解答:解:(1)f(x)是奇函数,
因为对于任意的x(x≠0),

所以f(x)是奇函数
(2)①当x>0时,f(x)的单调减区间为(0,2),
对于任意的x1,x2∈(0,2),当x1<x2时
 .
.因为0<x1x2<4,所以f(x1)-f(x2)>0
所以f(x)在(0,2)上为减函数
②当x>0时,f(x)的单调增区间为(2,+∞),
对于任意的x1,x2∈(2,+∞),当x1<x2时

因为x1x2>4,所以f(x1)-f(x2)<0
所以f(x)在(2,+∞)上为增函数
点评:本题主要考查了证明函数奇偶性的方法,利用函数单调性的定义证明函数单调性的方法步骤,代数变形能力和逻辑推理能力

练习册系列答案
相关题目
 且
且
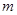 的值;(2)判定
的值;(2)判定 的奇偶性;
的奇偶性;
 ,
, .
. .
.