题目内容
已知O为坐标原点,点A(2,0),B(0,2),C(cosα,sinα),且0<α<π.
(Ⅰ)若 ,求tanα的值;
,求tanα的值;
(Ⅱ)若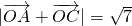 ,求
,求 与
与 的夹角.
的夹角.
解:(1)∵ =(cosα-2,sinα)•(cosα,sinα-2)=cos2α-2cosα+sin2α-2sinα
=(cosα-2,sinα)•(cosα,sinα-2)=cos2α-2cosα+sin2α-2sinα
=1-2cosα-2sinα= ,
,
且 0<α<π,∴sinα+cosα= .
.
再由 cos2α+sin2α=1 可得 cosα=- ,sinα=
,sinα= ,故
,故 .
.
(2)∵ =(2+cosα,sinα),
=(2+cosα,sinα),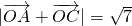 ,
,
∴4+4cosα+cos2α+sin2α=7,解得cosα= ,
,
∴α= .
.
分析:(1)先由 =
= ,求出sinα+cosα=
,求出sinα+cosα= ,再根据再cos2α+sin2α=1以及α的范围,可得
,再根据再cos2α+sin2α=1以及α的范围,可得
cosα和sinα的值,从而求得tanα的值.
(2)由 =(2+cosα,sinα),
=(2+cosα,sinα),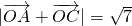 ,求得cosα=
,求得cosα= ,从而求得α的值.
,从而求得α的值.
点评:本题主要考查两个向量的数量积公式的应用,向量的模的定义,求向量的模的方法,属于中档题.
 =(cosα-2,sinα)•(cosα,sinα-2)=cos2α-2cosα+sin2α-2sinα
=(cosα-2,sinα)•(cosα,sinα-2)=cos2α-2cosα+sin2α-2sinα=1-2cosα-2sinα=
 ,
,且 0<α<π,∴sinα+cosα=
 .
.再由 cos2α+sin2α=1 可得 cosα=-
 ,sinα=
,sinα= ,故
,故 .
.(2)∵
 =(2+cosα,sinα),
=(2+cosα,sinα),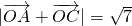 ,
,∴4+4cosα+cos2α+sin2α=7,解得cosα=
 ,
,∴α=
 .
.分析:(1)先由
 =
= ,求出sinα+cosα=
,求出sinα+cosα= ,再根据再cos2α+sin2α=1以及α的范围,可得
,再根据再cos2α+sin2α=1以及α的范围,可得cosα和sinα的值,从而求得tanα的值.
(2)由
 =(2+cosα,sinα),
=(2+cosα,sinα),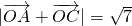 ,求得cosα=
,求得cosα= ,从而求得α的值.
,从而求得α的值.点评:本题主要考查两个向量的数量积公式的应用,向量的模的定义,求向量的模的方法,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目