题目内容
已知函数
是奇函数，且
（1）求
的值；
（2）指出函数
的单调区间，并加以证明.
解：（1）由
是奇函数，知
即有
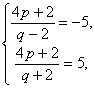解得
（2）由（1）得
设
则
当
时，
即
函数在
上是增函数.
当
时，
即
函数在
上是减函数.
由为奇函数，知函数在
上是增函数，
函数在
上是减函数.
练习册系列答案
相关题目
题目内容
已知函数是奇函数，且
（1）求的值；
（2）指出函数的单调区间，并加以证明.
解：（1）由是奇函数，知即有
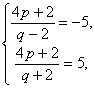解得
（2）由（1）得
设则
当时，即函数在上是增函数.
当时，即
函数在上是减函数.
由为奇函数，知函数在上是增函数，
函数在上是减函数.
是奇函数，且
，
的值；
在区间
上是减函数. 
是奇函数，且在区间
上单调递减，则
上是（ ） 
B. 单调递减函数，且有最大值
D.
单调递增函数，且有最大值
是奇函数，且
.
上的单调性，并加以证明. 
是奇函数，且图像在点
为自然对数的底数）处的切线斜率为3.
、
的值;
，且
对任意
恒成立，求
的最大值;
时，证明：
是奇函数，且满足
、
的值；
在区间
单调递减，在区间
单调递增；
同时满足以下两个条件：1不等式
对
恒成立；
2方程
在
上有解．若存在，试求出实数