Question

如图,圆x²+y²=4与y轴的两个交点分别为A、B.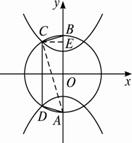

以A、B为焦点,坐标轴为对称轴的双曲线与圆在y轴左方的交点分别为C、D.当梯形ABCD的周长最大时,求此双曲线的方程.

Answer 1

解析:设双曲线的方程为-=1(a>0,b>0),C(x₀,y₀)(x₀<0,y₀>0),|BC|=t(0).

连结AC,则∠ACB=90°.

作CE⊥AB于E,则有|BC|²=|BE|·|AB|,

∴t²=(2-y₀)×4,即y₀=2-.

∴梯形ABCD的周长l=4+2t+2y₀.

即l=-t²+2t+8=-(t-2)²+10.

当t=2时,l最大.

此时|BC|=2,|AC|=2.

又C在双曲线的上支上,且B、A分别为上、下两焦点,

∴|AC|-|BC|=2a,即2a=2-2.

∴a=3-1,即a²=4-2.

∴b²=c²-a²=2.

∴所求双曲线方程为-=1.