题目内容
如果关于实数x的方程 的所有解中,仅有一个正数解,那么实数a的取值范围为________.
的所有解中,仅有一个正数解,那么实数a的取值范围为________.
(-∞,0]∪{2}
分析:由函数的定义域为(-∞,0)∪(0,+∞),故我们可将关于x的方程 有且仅有一个正实数解,转化为“双曲线 y1=1x与y2=3x-ax2的图象在y轴右侧只有一个交点”.对参数的取值范围进行讨论,求出实数a的取值范围
有且仅有一个正实数解,转化为“双曲线 y1=1x与y2=3x-ax2的图象在y轴右侧只有一个交点”.对参数的取值范围进行讨论,求出实数a的取值范围
解答:将方程 改写为
改写为 ,令
,令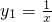 ,y2=3x-ax2.
,y2=3x-ax2.
“关于实数x的方程 的所有解中,仅有一个正数解”等价于“双曲线
的所有解中,仅有一个正数解”等价于“双曲线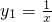 与y2=3x-ax2的图象在y轴右侧只有一个交点”.
与y2=3x-ax2的图象在y轴右侧只有一个交点”.
双曲线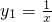 在第一、三象限内.
在第一、三象限内.
当a>0时,抛物线y2=3x-ax2的开口向下且过原点(0,0)及x轴正半轴上的点 ,研究知,当a<2时,双曲线
,研究知,当a<2时,双曲线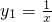 与抛物线y2=3x-ax2在第一象限内有两个交点,当a>2时,两曲线在第一象限无交点,当a=2进,两曲线仅有一个交点,故a=2符合题意.
与抛物线y2=3x-ax2在第一象限内有两个交点,当a>2时,两曲线在第一象限无交点,当a=2进,两曲线仅有一个交点,故a=2符合题意.
当a=0时,y2=3x-ax2=3x为直线,此时,双曲线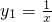 与直线y2=3x在第一象限内只有一个交点,故a=0符合题意.
与直线y2=3x在第一象限内只有一个交点,故a=0符合题意.
当a<0时,抛物线y2=3x-ax2的开口向上且过原点(0,0)及x轴负半轴上的点 ,此时,双曲线
,此时,双曲线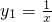 与抛物线y2=3x-ax2在第一象限内仅有一个交点,故a<0符合题意.
与抛物线y2=3x-ax2在第一象限内仅有一个交点,故a<0符合题意.
综上所述,实数a的取值范围为(-∞,0]∪{2}.
故答案为:(-∞,0]∪{2}.
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据函数的定义域,将分式方程根的个数问题转化为两曲线的交点个数问题是解答本题的关键.属中档题.
分析:由函数的定义域为(-∞,0)∪(0,+∞),故我们可将关于x的方程
 有且仅有一个正实数解,转化为“双曲线 y1=1x与y2=3x-ax2的图象在y轴右侧只有一个交点”.对参数的取值范围进行讨论,求出实数a的取值范围
有且仅有一个正实数解,转化为“双曲线 y1=1x与y2=3x-ax2的图象在y轴右侧只有一个交点”.对参数的取值范围进行讨论,求出实数a的取值范围解答:将方程
 改写为
改写为 ,令
,令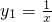 ,y2=3x-ax2.
,y2=3x-ax2.“关于实数x的方程
 的所有解中,仅有一个正数解”等价于“双曲线
的所有解中,仅有一个正数解”等价于“双曲线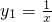 与y2=3x-ax2的图象在y轴右侧只有一个交点”.
与y2=3x-ax2的图象在y轴右侧只有一个交点”.双曲线
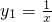 在第一、三象限内.
在第一、三象限内.当a>0时,抛物线y2=3x-ax2的开口向下且过原点(0,0)及x轴正半轴上的点
 ,研究知,当a<2时,双曲线
,研究知,当a<2时,双曲线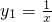 与抛物线y2=3x-ax2在第一象限内有两个交点,当a>2时,两曲线在第一象限无交点,当a=2进,两曲线仅有一个交点,故a=2符合题意.
与抛物线y2=3x-ax2在第一象限内有两个交点,当a>2时,两曲线在第一象限无交点,当a=2进,两曲线仅有一个交点,故a=2符合题意.当a=0时,y2=3x-ax2=3x为直线,此时,双曲线
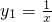 与直线y2=3x在第一象限内只有一个交点,故a=0符合题意.
与直线y2=3x在第一象限内只有一个交点,故a=0符合题意.当a<0时,抛物线y2=3x-ax2的开口向上且过原点(0,0)及x轴负半轴上的点
 ,此时,双曲线
,此时,双曲线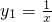 与抛物线y2=3x-ax2在第一象限内仅有一个交点,故a<0符合题意.
与抛物线y2=3x-ax2在第一象限内仅有一个交点,故a<0符合题意.综上所述,实数a的取值范围为(-∞,0]∪{2}.
故答案为:(-∞,0]∪{2}.
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据函数的定义域,将分式方程根的个数问题转化为两曲线的交点个数问题是解答本题的关键.属中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目