题目内容
已知△ABC的面积为1,设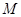 是△
是△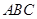 内的一点(不在边界上),定义
内的一点(不在边界上),定义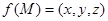 ,其中
,其中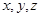 分别表示△
分别表示△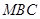 ,△
,△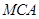 ,△
,△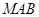 的面积,若
的面积,若 ,则
,则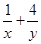 的最小值为( )
的最小值为( )
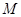 是△
是△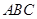 内的一点(不在边界上),定义
内的一点(不在边界上),定义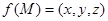 ,其中
,其中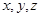 分别表示△
分别表示△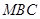 ,△
,△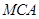 ,△
,△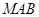 的面积,若
的面积,若 ,则
,则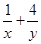 的最小值为( )
的最小值为( ) | A.8 | B.9 | C.16 | D.18 |
D
解:∵ AB • AC =2 ,∠BAC=30°,
,∠BAC=30°,
所以由向量的数量积公式得| AB | •| AC | •cos∠BAC=2 ,
,
∴| AB || AC |=4,
∵S△ABC | AB | •| AC |•sin∠BAC=1,
| AB | •| AC |•sin∠BAC=1,
由题意得,
x+y=1- =
= .
.
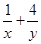 =2(
=2(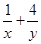 )(x+y)=2(5+
)(x+y)=2(5+ )≥2(5+2
)≥2(5+2 )=18,等号在x=
)=18,等号在x= ,y=
,y= 取到,所以最小值为18.
取到,所以最小值为18.
故选C
 ,∠BAC=30°,
,∠BAC=30°,所以由向量的数量积公式得| AB | •| AC | •cos∠BAC=2
 ,
,∴| AB || AC |=4,
∵S△ABC
 | AB | •| AC |•sin∠BAC=1,
| AB | •| AC |•sin∠BAC=1,由题意得,
x+y=1-
 =
= .
.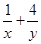 =2(
=2(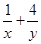 )(x+y)=2(5+
)(x+y)=2(5+ )≥2(5+2
)≥2(5+2 )=18,等号在x=
)=18,等号在x= ,y=
,y= 取到,所以最小值为18.
取到,所以最小值为18.故选C

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为 、
、 、
、 ,若
,若 .
. ,求
,求




 中,
中, ,
, .
. 的大小;
的大小; ,求最小边的边长.
,求最小边的边长. B.北偏东40°;10
B.北偏东40°;10
 中,若角
中,若角 ,
, ,则
,则 ,
, ,S△ABC=4
,S△ABC=4 ,那么
,那么 =( )
=( )



 中,
中, ,那么角A等于( )
,那么角A等于( )