题目内容

对于函数y=f（x）（x∈D,D是此函数的定义域），若同时满足下列条件：

①f（x）在D内单调递增或递减;

②存在区间［a，b］D,使f（x）在［a，b］上的值域为［a，b］，则把y=f（x）（x∈D）叫闭函数.

（1）求闭函数y=-x3符合条件②的区间［a，b］;

（2）y=k+是闭函数，求实数k的取值范围.

解：（1）∵y=-x3为［a，b］上的减函数，

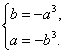∴又a＜b，∴

∴所求区间为［-1，1］.

（2）设函数y=k+符合条件②的区间为［a，b］，

则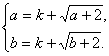

∴a、b为方程x=k+的两实根.

命题等价于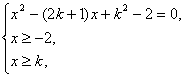

有两个不等实根.

当k≤-2时，

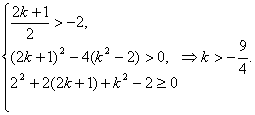
∴-＜k≤-2.

当k＞-2时,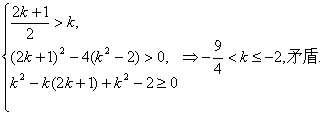

∴k∈（-，-2］.

练习册系列答案
相关题目
已知y=f（x）是定义在R上的奇函数，且y=f(x+
π
2
)为偶函数，对于函数y=f（x）有下列几种描述：
①y=f（x）是周期函数②x=π是它的一条对称轴；③（-π，0）是它图象的一个对称中心；
④当x=
π
2
时，它一定取最大值；其中描述正确的是
 
．
给出下列五个命题：
①函数y=f（x），x∈R的图象与直线x=a可能有两个不同的交点；
②函数y=log2x2与函数y=2log2x是相等函数；
③对于指数函数y=2x与幂函数y=x2，总存在x0，当x＞x0 时，有2x＞x2成立；
④对于函数y=f（x），x∈[a，b]，若有f（a）•f（b）＜0，则f（x）在（a，b）内有零点．
⑤已知x1是方程x+lgx=5的根，x2是方程x+10x=5的根，则x1+x2=5．
其中正确的序号是
③⑤
③⑤
．
（2010•和平区一模）函数y=f（x）是定义在[a，b]上的增函数，其中a，b∈R，且0＜b＜-a，已知y=f（x）无零点，设F（x）=f2（x）+f2（-x），则对于函数y=F（x）有如下四种说法：①定义域是[-b，b]；②最小值是0；③是偶函数；④在定义域内单调递增．其中正确的说法是（　　）
（2010•上海模拟）对于函数y=f（x）的图象上任意两点A（a，f（a）），B（b，f（b）），设点C分
AB
的比为λ（λ＞0）．若函数为f（x）=x2（x＞0），则直线AB必在曲线AB的上方，且由图象特征可得不等式
a2+λb2
1+λ
＞(
a+λb
1+λ
)2．若函数为f（x）=log2010x，请分析该函数的图象特征，上述不等式可以得到不等式
log2010a+log2010b
1+λ
＜log2010
a+λb
1+λ
log2010a+log2010b
1+λ
＜log2010
a+λb
1+λ
．
已知定义在区间[-3，3]上的函数y=f（x）满足f（-x）+f（x）=0，对于函数y=f（x）的图象上任意两点（x1，f（x1）），（x2，f（x2））都有（x1-x2）•[f（x1）-f（x2）]＜0．若实数a，b满足f（a2-2a）+f（2b-b2）≤0，则点（a，b）所在区域的面积为（　　）
A、8B、4C、2D、1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网