题目内容
已知二次函数f(x)=ax2+x,(a∈R)。
(1)当0<a< 时,f(sinx)(x∈R)的最大值为
时,f(sinx)(x∈R)的最大值为 ,求f(x)的最小值;
,求f(x)的最小值;
(2)对于任意的x∈R,总有|f(sinxcosx)|≤1。试求a的取值范围;
(3)若当n∈N*时,记 ,令a=1,求证:
,令a=1,求证: 成立。
成立。
(1)当0<a<
 时,f(sinx)(x∈R)的最大值为
时,f(sinx)(x∈R)的最大值为 ,求f(x)的最小值;
,求f(x)的最小值;(2)对于任意的x∈R,总有|f(sinxcosx)|≤1。试求a的取值范围;
(3)若当n∈N*时,记
 ,令a=1,求证:
,令a=1,求证: 成立。
成立。解:(1)由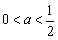 知
知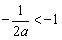
故当 时,f(x)取得最大值
时,f(x)取得最大值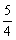
即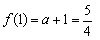
∴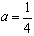
∴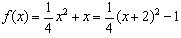
所以f(x)的最小值为-1。
(2)∵对于任意的x∈R,总有| |≤1
|≤1
令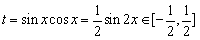
则命题转化为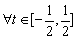 ,不等式
,不等式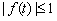 恒成立
恒成立
当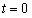 时,
时,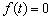 使
使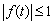 成立
成立
当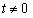 时,有
时,有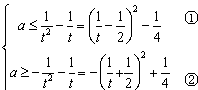
对于任意的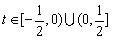 恒成立
恒成立
∵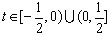
∴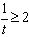 或
或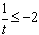
则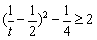
故要使①式成立,则有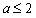
又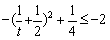
故要使②式成立,则有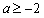
由题意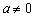
综上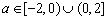 。
。
(3)由题意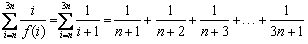
令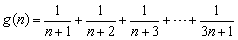
则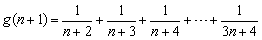
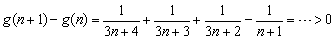
∴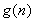 在
在 时单调递增
时单调递增
∴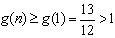
又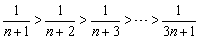
∴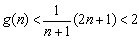
综上,原结论成立。
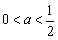 知
知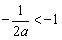
故当
 时,f(x)取得最大值
时,f(x)取得最大值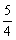
即
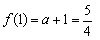
∴
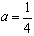
∴
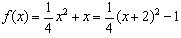
所以f(x)的最小值为-1。
(2)∵对于任意的x∈R,总有|
 |≤1
|≤1令
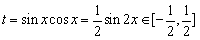
则命题转化为
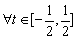 ,不等式
,不等式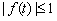 恒成立
恒成立当
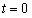 时,
时,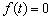 使
使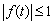 成立
成立当
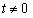 时,有
时,有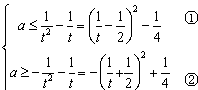
对于任意的
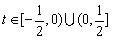 恒成立
恒成立∵
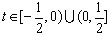
∴
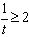 或
或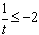
则
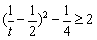
故要使①式成立,则有
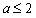
又
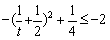
故要使②式成立,则有
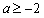
由题意
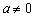
综上
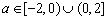 。
。(3)由题意
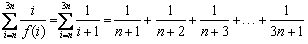
令
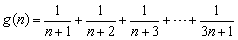
则
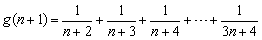
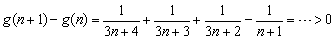
∴
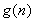 在
在 时单调递增
时单调递增∴
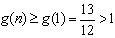
又
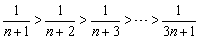
∴
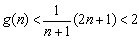
综上,原结论成立。

练习册系列答案
相关题目