题目内容
函数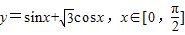 的最小值是 .
的最小值是 .
【答案】分析:利用辅助角公司可将y=sinx+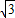 cosx化为f(x)=2sin(x+
cosx化为f(x)=2sin(x+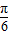 ),而x∈[0,
),而x∈[0,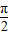 ],从而可求得f(x)的最小值.
],从而可求得f(x)的最小值.
解答:解:∵y=f(x)=sinx+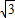 cosx=2sin(x+
cosx=2sin(x+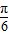 ),
),
又x∈[0,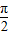 ],
],
∴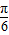 ≤x+
≤x+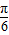 ≤
≤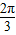 ,
,
∴1≤2sin(x+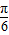 )≤2,
)≤2,
故答案为:1.
点评:本题考查两角和与差的正弦函数,考查正弦函数的单调性,考查三角函数的化简,属于中档题.
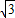 cosx化为f(x)=2sin(x+
cosx化为f(x)=2sin(x+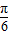 ),而x∈[0,
),而x∈[0,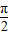 ],从而可求得f(x)的最小值.
],从而可求得f(x)的最小值.解答:解:∵y=f(x)=sinx+
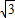 cosx=2sin(x+
cosx=2sin(x+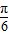 ),
),又x∈[0,
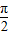 ],
],∴
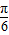 ≤x+
≤x+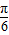 ≤
≤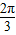 ,
,∴1≤2sin(x+
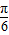 )≤2,
)≤2,故答案为:1.
点评:本题考查两角和与差的正弦函数,考查正弦函数的单调性,考查三角函数的化简,属于中档题.

练习册系列答案
相关题目
 函数f(x)在[-2,2]上的图象如图所示,则此函数的最小值是
函数f(x)在[-2,2]上的图象如图所示,则此函数的最小值是