题目内容
若函数f(x)为偶函数,且在(0,+∞)内是增函数,又f (-2013)=0,则不等式x•f(x)<0的集合是
- A.{x|x<-2013或x>2013}
- B.{x|-2013<x<0或x>2013}
- C.{x|x<-2013或0<x<2013}
- D.{x|-2013<x<0或0<x<2013}
C
分析:由偶函数在对称区间上单调性相反,可判断出函数的单调性,进而分x∈(-∞,0)和x∈(0,+∞)两种情况,分别求出使不等式x•f(x)<0的x的取值,最后综合分类讨论结果可得答案.
解答:∵函数f(x)为偶函数,且在(0,+∞)内是增函数,
∴函数f(x)在(-∞,0)内是减函数,
当x∈(-∞,0)时,若x•f(x)<0,则f(x)>0
∴x<-2013
当x∈(0,+∞)时,若x•f(x)<0,则f(x)<0
∴0<x<2013
故不等式x•f(x)<0的集合是{x|x<-2013或0<x<2013}
故选C
点评:本题考查的知识点是函数奇偶性与单调性的综合,其中根据偶函数在对称区间上单调性相反,判断出函数的单调性,是解答的关键.
分析:由偶函数在对称区间上单调性相反,可判断出函数的单调性,进而分x∈(-∞,0)和x∈(0,+∞)两种情况,分别求出使不等式x•f(x)<0的x的取值,最后综合分类讨论结果可得答案.
解答:∵函数f(x)为偶函数,且在(0,+∞)内是增函数,
∴函数f(x)在(-∞,0)内是减函数,
当x∈(-∞,0)时,若x•f(x)<0,则f(x)>0
∴x<-2013
当x∈(0,+∞)时,若x•f(x)<0,则f(x)<0
∴0<x<2013
故不等式x•f(x)<0的集合是{x|x<-2013或0<x<2013}
故选C
点评:本题考查的知识点是函数奇偶性与单调性的综合,其中根据偶函数在对称区间上单调性相反,判断出函数的单调性,是解答的关键.

练习册系列答案
相关题目
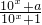 是奇函数.
是奇函数.