题目内容
对于二次函数f(x)=x2-ax+构建问题:对于二次函数f(x)=x2-ax+![]() (a∈R),求f(x)在[0,1]上的最小值g(a),并求g(a)的最大值.
(a∈R),求f(x)在[0,1]上的最小值g(a),并求g(a)的最大值.
解析:f(x)=(x-![]() )2+
)2+![]() -
-![]() ,
,
由x∈[0,1],故讨论对称轴x=![]() ,得
,得
g(a)=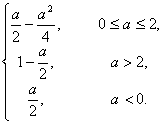
又∵当0≤a≤2时,
g(a)=-![]() (a-1)2+
(a-1)2+![]() ≤
≤![]() ;
;
当a>2时,g(a)=1-![]() <0;
<0;
当a<0时,g(a)=![]() <0.
<0.
∴g(a)max=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目