题目内容
过双曲线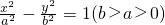
的左焦点F（-c，0）（c＞0）作圆x2+y2=a2的切线，切点为E，延长FE交双曲线右支于点P，若
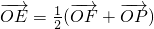（O是坐标原点），则双曲线的离心率为
- A.
- B.
- C.
- D.
A
分析：由题设知|EF|=b，|PF|=2b，|PF'|=2a，再由|PF|-|PF'|=2a，知b=2a，由此能求出双曲线的离心率．
解答：∵|OF|=c，|OE|=a，∴|EF|=b，
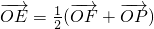∵，∴|PF|=2b，|PF'|=2a，
∵|PF|-|PF'|=2a，∴b=2a，∴
．
故选A．
点评：本题考查双曲线的性质和应用，解题时要认真审题，仔细解答．
分析：由题设知|EF|=b，|PF|=2b，|PF'|=2a，再由|PF|-|PF'|=2a，知b=2a，由此能求出双曲线的离心率．
解答：∵|OF|=c，|OE|=a，∴|EF|=b，
∵
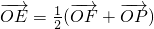，∴|PF|=2b，|PF'|=2a，∵|PF|-|PF'|=2a，∴b=2a，∴
．故选A．
点评：本题考查双曲线的性质和应用，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
的左焦点F作⊙O: 
的两条切线，记切点为A,B,双曲线左顶点为C，若
,则双曲线的离心率为____________.
的左焦点F的直线
与双曲线的左支交于A、B两点，且以线段AB为直径的圆被双曲线C的左准线截得的劣弧的弧度数为
，那么双曲线的离心率为
（B）
（C）2 （D）
的左焦点F的直线
与双曲线的左支交于A、B两点，且以线段AB为直径的圆被双曲线C的左准线截得的劣弧的弧度数为
，那么双曲线的离心率为
（B）
（C）2 （D）