题目内容
已知a>1,命题p:a(x-2)+1>0,命题q:(x-1)2>a(x-2)+1>0.若命题p、q同时成立,求x的取值范围.
解:依题意,有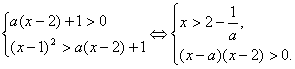
①若1<a<2时,则有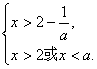
而a-![]() >0,即a>2-
>0,即a>2-![]() ,
,
∴x>2或2-![]() <x<a.
<x<a.
故此时x的取值范围为(2-![]() ,a)∪(2,+∞).
,a)∪(2,+∞).
②若a=2时,则x>![]() 且x≠2,
且x≠2,
此时x的取值范围为(![]() ,2)∪(2,+∞).
,2)∪(2,+∞).
③若a>2时,则有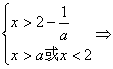 x>a或2-
x>a或2-![]() <x<2.
<x<2.
此时x的取值范围为(2-![]() ,2)∪(a,+∞).
,2)∪(a,+∞).
综上所述,当1<a<2时,x的取值范围为(2-![]() ,a)∪(2,+∞);
,a)∪(2,+∞);
当a=2时,x的取值范围为(![]() ,2)∪(2,+∞);
,2)∪(2,+∞);
当a>2时,x的取值范围为(2-![]() ,2)∪(a,?+∞).
,2)∪(a,?+∞).

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目