题目内容
如图,半径为1的圆O上有一定点P和两个动点A,B, AB=1,则 的最大值为( )
的最大值为( )

 的最大值为( )
的最大值为( )A. | B. | C.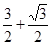 | D. |

A
连接OA、OB、OP,由| 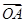 |="|"
|="|" 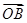 |=|
|=|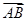 |=1知:∠AOB=
|=1知:∠AOB=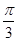 ,
,
设∠AOP=θ,则∠POB=θ+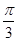 ,于是
,于是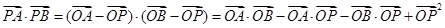
=1×1×cos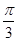 -1×1×cosθ-1×1×cos(θ+
-1×1×cosθ-1×1×cos(θ+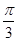 )+1==
)+1==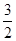 -[cosθ+cos(θ+
-[cosθ+cos(θ+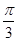 )]=
)]=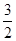 -
-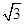 (
( cosθ-
cosθ-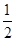 sinθ)=
sinθ)=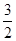 -
- 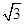 cos(θ+
cos(θ+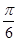 ),∴
),∴ 的最大值为
的最大值为 ,故选A
,故选A
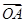 |="|"
|="|" 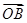 |=|
|=|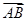 |=1知:∠AOB=
|=1知:∠AOB=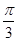 ,
,设∠AOP=θ,则∠POB=θ+
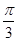 ,于是
,于是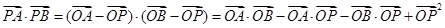
=1×1×cos
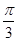 -1×1×cosθ-1×1×cos(θ+
-1×1×cosθ-1×1×cos(θ+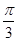 )+1==
)+1==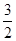 -[cosθ+cos(θ+
-[cosθ+cos(θ+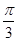 )]=
)]=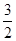 -
-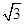 (
( cosθ-
cosθ-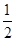 sinθ)=
sinθ)=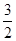 -
- 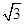 cos(θ+
cos(θ+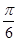 ),∴
),∴ 的最大值为
的最大值为 ,故选A
,故选A
练习册系列答案
相关题目
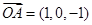 ,
,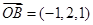 ,则以OA、OB为相邻两边的平行四边形的面积为 .
,则以OA、OB为相邻两边的平行四边形的面积为 .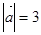 ,
,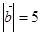 ,且
,且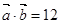 ,则
,则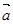 在
在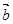 方向上的投影为_______________.
方向上的投影为_______________. 是边长为
是边长为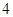 的正方形,动点
的正方形,动点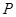 在以
在以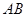 为直径的圆弧
为直径的圆弧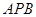 上,则
上,则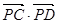 的取值范围是 ▲ ;
的取值范围是 ▲ ;  的正方形
的正方形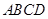 中,点
中,点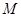 在
在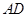 上,正方形
上,正方形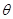 角
角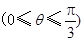 到
到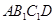 的位置,同时点
的位置,同时点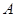 运动点
运动点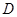 ,
,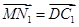 ,点
,点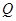 在
在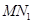 上,在运动过程中点
上,在运动过程中点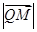
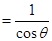 ,记点
,记点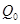 ,则在运动过程中向量
,则在运动过程中向量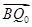 与
与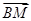 夹角
夹角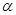 的正切值
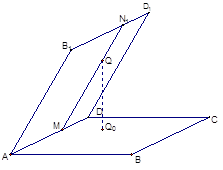
的正切值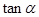 的最大值为 .
的最大值为 .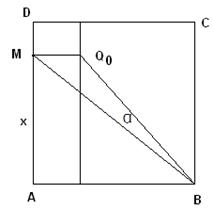
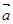 ,
,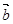 是非零向量,且
是非零向量,且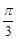 ,则向量
,则向量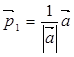 与
与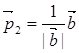 的夹角为 .
的夹角为 .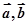 满足
满足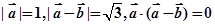 ,则
,则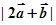 =( )
=( ) 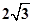
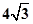
 中,
中, =3,
=3, ,则
,则 与
与 夹角的取值范围是( )
夹角的取值范围是( )



 ,
, 满足
满足 则
则 ( )
( )