题目内容

已知函数f（x）在定义域（-∞，0]内存在反函数，且f（x-1）=x²-2x，则 $数学公式$ =________．

$\text{[math]}$
分析：欲求 $\text{[math]}$ 的值，根据反函数的定义知，只须求方程f（x）=- $\text{[math]}$ 的解x的值，故先由f（x-1）=x²-2x，求出f（x）即可．
解答：∵f（x-1）=x²-2x=（x-1）²-1，
∴f（x）=x²-1，且x∈（-∞，0]，
令f（x）=- $\text{[math]}$ ，得：x=- $\text{[math]}$ ，或x= $\text{[math]}$ （正值舍掉）
∴ $\text{[math]}$ =- $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本小题主要考查反函数以及互为反函数之间的关系、函数解析式的求法等基础知识，考查运算求解能力与转化思想．属于基础题．

练习册系列答案

认知规律训练法系列答案

钟书金牌期末冲刺100分系列答案

重难点突破训练系列答案

万唯中考预测卷系列答案

初中英语听力课堂系列答案

周测月考单元评价卷系列答案

中学生英语随堂演练及单元要点检测题系列答案

中学单元测试卷系列答案

中领航深度衔接时效卷系列答案

智慧讲堂系列答案

相关题目

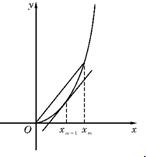已知函数f（x）=x³+x²，数列|x_n|（x_n＞0）的第一项x_n=1，以后各项按如下方式取定：曲线x=f（x）在（x_n+1，f（x_n+1））处的切线与经过（0，0）和（x_n，f （x_n））两点的直线平行（如图）．
求证：当n∈N^*时，
（Ⅰ）x_n²+x_n=3x_n+1²+2x_n+1；
（Ⅱ）(

已知函数f（x）=x³-x，其图象记为曲线C．
（1）求函数f（x）的单调区间；
（2）证明：若对于任意非零实数x₁，曲线C与其在点P₁（x₁，f（x₁））处的切线交于另一点P₂（x₂，f（x₂）），曲线C与其在点P₂（x₂，f（x₂））处的切线交于另一点P₃（x₃，f（x₃）），线段P₁P₂，P₂P₃与曲线C所围成封闭图形的面积分别记为S₁，S₂，则

下列说法正确的有（　　）个．
①已知函数f（x）在（a，b）内可导，若f（x）在（a，b）内单调递增，则对任意的?x∈（a，b），有f′（x）＞0．
②函数f（x）图象在点P处的切线存在，则函数f（x）在点P处的导数存在；反之若函数f（x）在点P处的导数存在，则函数f（x）图象在点P处的切线存在．
③因为3＞2，所以3+i＞2+i，其中i为虚数单位．
④定积分定义可以分为：分割、近似代替、求和、取极限四步，对求和In=

f(ξi)△x中ξ_i的选取是任意的，且I_n仅于n有关．
⑤已知2i-3是方程2x²+px+q=0的一个根，则实数p，q的值分别是12，26．

已知函数f（x）=ax+

-a（a∈R，a≠0）在x=3处的切线方程为（2a-1）x-2y+3=0
（1）若g（x）=f（x+1），求证：曲线g（x）上的任意一点处的切线与直线x=0和直线y=ax围成的三角形面积为定值；
（2）若f（3）=3，是否存在实数m，k，使得f（x）+f（m-x）=k对于定义域内的任意x都成立；
（3）若方程f（x）=t（x²-2x+3）|x|有三个解，求实数t的取值范围．

下列说法正确的有（）个．
①已知函数f（x）在（a，b）内可导，若f（x）在（a，b）内单调递增，则对任意的?x∈（a，b），有f′（x）＞0．
②函数f（x）图象在点P处的切线存在，则函数f（x）在点P处的导数存在；反之若函数f（x）在点P处的导数存在，则函数f（x）图象在点P处的切线存在．
③因为3＞2，所以3+i＞2+i，其中i为虚数单位．
④定积分定义可以分为：分割、近似代替、求和、取极限四步，对求和

中ξ_i的选取是任意的，且I_n仅于n有关．
⑤已知2i-3是方程2x²+px+q=0的一个根，则实数p，q的值分别是12，26．
A．0
B．1
C．3
D．4