题目内容
计算下列各式的值：（1）lg14-2lg
+lg7-lg18；（2）
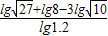；（3）（lg5）2+lg2•lg50．
【答案】分析：利用logaM+logaN=logaMN，logaM-logaN=loga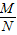
，以及对数运算性质log（an）Nm=
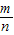logaN，我们易将式子进行化简，进而得到结果．
解答：解 （1）法一 lg14-2lg
+lg7-lg18
=lg（2×7）-2（lg7-lg3）+lg7-lg（32×2）
=lg2+lg7-2lg7+2lg3+lg7-2lg3-lg2=0．
法二 lg14-2lg
+lg 7-lg18
=lg14-lg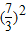
+lg7-lg18=lg
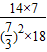=lg1=0．
（2）
=
=
=
=
．
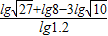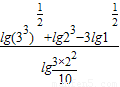
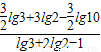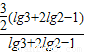（3）原式=（lg5）2+lg2•（lg2+2lg5）
=（lg5）2+2lg5•lg2+（lg2）2
=（lg5+lg2）2=1．
点评：本题考查的知识点是对数的运算性质，换底公式，熟练掌握对数的运算性质及换底公式及其推论是解答对数化简求值类问题的关键．
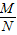，以及对数运算性质log（an）Nm=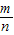logaN，我们易将式子进行化简，进而得到结果．解答：解 （1）法一 lg14-2lg
+lg7-lg18=lg（2×7）-2（lg7-lg3）+lg7-lg（32×2）
=lg2+lg7-2lg7+2lg3+lg7-2lg3-lg2=0．
法二 lg14-2lg
+lg 7-lg18=lg14-lg
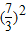+lg7-lg18=lg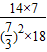=lg1=0．（2）
==
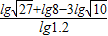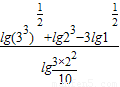
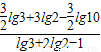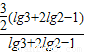==．（3）原式=（lg5）2+lg2•（lg2+2lg5）
=（lg5）2+2lg5•lg2+（lg2）2
=（lg5+lg2）2=1．
点评：本题考查的知识点是对数的运算性质，换底公式，熟练掌握对数的运算性质及换底公式及其推论是解答对数化简求值类问题的关键．
练习册系列答案
相关题目