Question

已知函数f（x）=

1

3

x3+

1

2

ax2+2bx+c（a，b，c∈R）在区间（0，1）内取得极大值在区间（1，2）内取得极小值，则

(a+3)2+b2

的取值范围为（　　）

• A．（

  2

  2

  ，2）
• B．（

  1

  2

  ，4）
• C．（1，2）
• D．（1，4）

Answer 1

分析：先求导函数，由已知得到a，b的取值范围，再由线性规划得到所求值即可．

解答：解：由于f(x)=

1

3

x3+

1

2

ax2 +2bx+c，则f’（x）=x²+ax+2b
又由函数f（x）在区间（0，1）内取得极大值在区间（1，2）内取得极小值，
则

f′(0)＞0   f′(1)＜0   f′(2)＞0

亦即

a+b+2＞0   a+2b+1＜0   b＞0

得到可行域如下图所示，

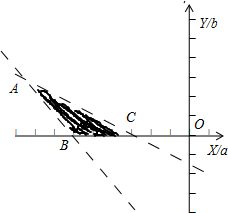
则B（-2，0），C（-1，0），A（-3，1）
又由

(a+3)2+b2

表示阴影部分内的点（-3，0）点的距离，
故

(a+3)2+b2

的取值范围是（

2

2

，2）
故答案为A．

点评：本题考查线性规划问题与导数在研究函数极值的应用，属于基础题．