题目内容
先将函数 的图象向左平移
的图象向左平移 个长度单位,再保持所有点的纵坐标不变
个长度单位,再保持所有点的纵坐标不变
横坐标压缩为原来的 ,得到函数
,得到函数 的图象,则使
的图象,则使 为增函数的一个区间是
为增函数的一个区间是
 的图象向左平移
的图象向左平移 个长度单位,再保持所有点的纵坐标不变
个长度单位,再保持所有点的纵坐标不变横坐标压缩为原来的
 ,得到函数
,得到函数 的图象,则使
的图象,则使 为增函数的一个区间是
为增函数的一个区间是 A. | B. | C. | D. |
A
根据函数图象平移公式和三角变换公式,可得g(x)= cos4x,再用余弦函数单调区间的结论即可得到本题答案.
cos4x,再用余弦函数单调区间的结论即可得到本题答案.
解:∵f(x)=sinxcosx= sin2x
sin2x
∴f(x)的图象向左平移 个长度单位,可得y=f(x+
个长度单位,可得y=f(x+ )=
)= sin(2x+
sin(2x+ )=
)= cos2x
cos2x
再保持所有点的纵坐标不变横坐标压缩为原来的 ,可得
,可得
g(x)= cos4x
cos4x
令-π+2kπ≤4x≤2kπ(k∈Z),可得x∈(- +
+ kπ,
kπ, kπ)(k∈Z),
kπ)(k∈Z),
由此可得g(x)的增区间为(- +
+ kπ,
kπ, kπ)(k∈Z),
kπ)(k∈Z),
再取k=1,得( ,
, ),因此A项符合题意
),因此A项符合题意
故选:A
 cos4x,再用余弦函数单调区间的结论即可得到本题答案.
cos4x,再用余弦函数单调区间的结论即可得到本题答案.解:∵f(x)=sinxcosx=
 sin2x
sin2x∴f(x)的图象向左平移
 个长度单位,可得y=f(x+
个长度单位,可得y=f(x+ )=
)= sin(2x+
sin(2x+ )=
)= cos2x
cos2x再保持所有点的纵坐标不变横坐标压缩为原来的
 ,可得
,可得g(x)=
 cos4x
cos4x令-π+2kπ≤4x≤2kπ(k∈Z),可得x∈(-
 +
+ kπ,
kπ, kπ)(k∈Z),
kπ)(k∈Z),由此可得g(x)的增区间为(-
 +
+ kπ,
kπ, kπ)(k∈Z),
kπ)(k∈Z),再取k=1,得(
 ,
, ),因此A项符合题意
),因此A项符合题意故选:A

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,如
,如 .已知
.已知 ,
, ,则
,则
 ( )
( ) 



 <
< ,则函数y=
,则函数y= 的值域为
的值域为 )
) )
) =( )
=( )

 的图象向右平移
的图象向右平移 个单位后,图象关于直线
个单位后,图象关于直线 对称, 则m最小值为 .
对称, 则m最小值为 . 则
则 ____________
____________
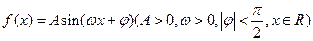 在一个周期内的图像如图所示
在一个周期内的图像如图所示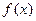 的
的 解析式;
解析式;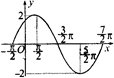
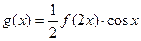 ,求,
,求,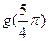 的值
的值