题目内容
“m= ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )A.充分必要条件
B.充分而不必要条件
C.必要而不充分条件
D.既不充分也不必要条件
【答案】分析:判断充分性只要将“m= ”代入各直线方程,看是否满足(m+2)(m-2)+3m•(m+2)=0,判断必要必看(m+2)(m-2)+3m•(m+2)=0的根是否只有
”代入各直线方程,看是否满足(m+2)(m-2)+3m•(m+2)=0,判断必要必看(m+2)(m-2)+3m•(m+2)=0的根是否只有
解答:解:当m= 时直线(m+2)x+3my+1=0的斜率是
时直线(m+2)x+3my+1=0的斜率是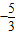 直线(m-2)x+(m+2)y-3=0的斜率是
直线(m-2)x+(m+2)y-3=0的斜率是
∴满足k1•k2=-1
∴“m= ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的充分条件,
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的充分条件,
而当(m+2)(m-2)+3m•(m+2)=0得:m= 或m=-2
或m=-2
∴“m= ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”充分而不必要条件.
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”充分而不必要条件.
故选B
点评:本题是通过常用逻辑用语考查两直线垂直的判定.
 ”代入各直线方程,看是否满足(m+2)(m-2)+3m•(m+2)=0,判断必要必看(m+2)(m-2)+3m•(m+2)=0的根是否只有
”代入各直线方程,看是否满足(m+2)(m-2)+3m•(m+2)=0,判断必要必看(m+2)(m-2)+3m•(m+2)=0的根是否只有
解答:解:当m=
 时直线(m+2)x+3my+1=0的斜率是
时直线(m+2)x+3my+1=0的斜率是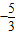 直线(m-2)x+(m+2)y-3=0的斜率是
直线(m-2)x+(m+2)y-3=0的斜率是
∴满足k1•k2=-1
∴“m=
 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的充分条件,
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的充分条件,而当(m+2)(m-2)+3m•(m+2)=0得:m=
 或m=-2
或m=-2∴“m=
 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”充分而不必要条件.
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”充分而不必要条件.故选B
点评:本题是通过常用逻辑用语考查两直线垂直的判定.

练习册系列答案
相关题目
下列命题中是假 命题的是( )
| A、对于命题p:?x∈R,使得x2+x+1<0,则?p:?x∈R,均有x2+x+1≥0 | ||
| B、抛物线y2=2x的焦点到准线的距离为1 | ||
C、“m=
| ||
| D、直线与抛物线只有一个交点是直线与抛物线相切的必要不充分条件 |