Question

(本小题满分12分)如图，已知直三棱柱ABC—A₁B₁C₁的侧棱长为2，底面△ABC是等腰直角三角形，且∠ACB=90°，AC=2，D是A A₁的中点． （Ⅰ）求异面直线AB和C₁D所成的角（用反三角函数表示）；（Ⅱ）若E为AB上一点，试确定点E在AB上的位置，使得A₁E⊥C₁D；

（Ⅲ）在（Ⅱ）的条件下，求点D到平面B₁C₁E的距离．

Answer 1

（Ⅰ）  （Ⅲ）DH=

解析:

[解析]（Ⅰ）法一：取CC₁的中点F，连接AF，BF，

则AF∥C₁D．      ∴∠BAF为异面直线AB与C₁D

所成的角或其补角． ∵△ABC为等腰直角三角形，AC=2，

∴AB=．又∵CC₁=2，∴AF=BF=．

∵cos∠BAF=， ∴∠BAF=，

即异面直线AB与C₁D所成的角为

法二：以C为坐标原点，CB，CA，CC₁分别为x轴，y轴，

z轴建立空间直角坐标系，

则A（0，2，0），B（2，0，0），C₁（0，0，2），

D（0，2，1），∴=（2，－2，0），=（0，2，－1）．

由于异面直线AB与C₁D所成的角为向量与的夹角或其补角． 设与的夹角为，

则cos==，∴=，即异面直线AB与C₁D所成的角为．

（Ⅱ）法一：过C₁作C₁M⊥A₁B₁，垂足为M，则M为A₁B₁的中点，且C₁M⊥平面AA₁B₁B．连接DM.

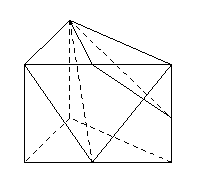∴DM即为C₁D在平面AA₁B₁B上的射影． 要使得A₁E⊥C₁D，

由三垂线定理知，只要A₁E⊥DM．  

∵AA₁=2，AB=2，由计算知，E为AB的中点．

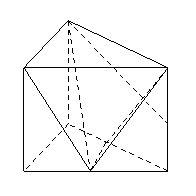法二：过E作EN⊥AC，垂足为N，则EN⊥平面AA₁C₁C.连接A₁N. ∴A₁N即为A₁E在平面AA₁C₁C上的射影．

要使得A₁E⊥C₁D，由三垂线定理知，只要A₁N⊥C₁D．

∵四边形AA₁C₁C为正方形，∴N为AC的中点，

∴E点为AB的中点．

法三：以C为坐标原点，CB，CA，CC₁分别为x轴，

y轴，z轴建立空间直角坐标系，则A₁（0，2，2），B（2，0，0），C₁（0，0，2），  D（0，2，1），

设E点的坐标为（x，y，0）,要使得A₁E⊥C₁D，

只要·=0， ∵=（x，y－2，－2)，

=（0，2，－1），∴y=1．

又∵点E在AB上，

∴∥．∴x=1．

∴E点为AB的中点．

（Ⅲ）法一：取AC中点N，连接EN，C₁N，

 则EN∥B₁C₁．     ∵B₁C₁⊥平面AA₁C₁C，

∴面B₁C₁NE⊥平面AA₁C₁C．     

过点D作DH⊥C₁N，垂足为H，则DH⊥平面B₁C₁NE，   

 ∴DH的长度即为点D到平面B₁C₁E的距离． 

在正方形AA₁C₁C中，

由计算知DH=，  即点D到平面B₁C₁E的距离.