题目内容
已知正项数列 中,
中, ,点
,点 在抛物线
在抛物线 上;数列
上;数列 中,点
中,点 在过点(0, 1),以
在过点(0, 1),以 为斜率的直线上。
为斜率的直线上。
(1)求数列 的通项公式;
的通项公式;
(2)若 , 问是否存在
, 问是否存在 ,使
,使 成立,若存在,求出
成立,若存在,求出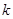 值;若不存在,说明理由;
值;若不存在,说明理由;
(3)对任意正整数 ,不等式
,不等式 恒成立,求正数
恒成立,求正数 的取值范围。
的取值范围。
(1) ,
,
(2)
(3)
解析试题分析:解:(1) 点
点 在二次函数
在二次函数 的图象上
的图象上 .. 2分
.. 2分
 .4
.4
(2). 
当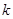 为偶数时,
为偶数时,  为奇数
为奇数 6
6
当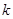 为奇数时,
为奇数时, 为偶数,
为偶数, (舍去)
(舍去)
综上,存在唯一的 符合条件. ..8
符合条件. ..8
(3) 由
得:  9
9
记: 10
10

 , 即
, 即 递增 13
递增 13
 14分
14分
考点:函数与不等式
点评:主要是考查了函数的性质,函数与不等式的综合运用,属于难度题。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 的图像与函数h(x)=x++2的图像关于点A(0,1)对称.
的图像与函数h(x)=x++2的图像关于点A(0,1)对称.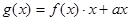 ,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间[0,2]上为减函数,求实数a的取值范围. ,若存在
,若存在 ,使得
,使得 ,则称
,则称 .
.  时,求函数
时,求函数 的不动点;
的不动点; ,函数
,函数 的取值范围;
的取值范围; 两点的横坐标是函数
两点的横坐标是函数 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围. 的最大值;
的最大值;  是否有实数解 .
是否有实数解 . 的空气隔层.根据热传导知识,对于厚度为
的空气隔层.根据热传导知识,对于厚度为 的均匀介质,两侧的温度差为
的均匀介质,两侧的温度差为 ,单位时间内,在单位面积上通过的热量
,单位时间内,在单位面积上通过的热量 ,其中
,其中 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为
为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为 ,空气的热传导系数为
,空气的热传导系数为 .)
.)
 ,
, ,内层玻璃外侧温度为
,内层玻璃外侧温度为 ,外层玻璃内侧温度为
,外层玻璃内侧温度为 ,且
,且 .试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用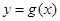 的导函数的图像与直线
的导函数的图像与直线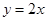 平行,且
平行,且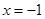 处取得极小值
处取得极小值 .设
.设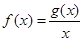 .
.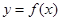 上的点
上的点 到点
到点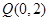 的距离的最小值为
的距离的最小值为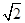 ,求
,求 的值;
的值; 如何取值时,函数
如何取值时,函数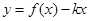 存在零点,并求出零点.
存在零点,并求出零点.
 .
.  时取得极值?说明理由;
时取得极值?说明理由; ,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.
,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.