题目内容
已知数列{an}的前n项和为Sn,a1=
,且2Sn=2Sn-1+2an-1+1(n≥2,n∈N*).数列{bn}满足b1=
,且3bn-bn-1=n(n≥2,n∈N*).(1)求证:数列{an}为等差数列;
(2)求证:数列{bn-an}为等比数列;
(3)求数列{bn}的通项公式以及前n项和Tn.
(1)证明:由an+1=2an-an-1(n≥2,n∈N*),
可得an+1-an=an-an-1(n≥2).
即an+1-an=an-an-1=…=a2-a1.
可知数列{an}为等差数列.
(2)证明:∵{an}为等差数列,
∴公差d=a2-a1=.
∴an=a1+(n-1)×=
n
.
又3bn-bn-1=n(n≥2),
∴bn=
bn-1+
n(n≥2).
∴bn-an=
bn-1+
n
n+
=
bn-1
n+
=
(bn-1
n+
)
=
［bn-1
(n-1)+
］
=
(bn-1-an-1).
又b1-a1≠0,
∴对n∈N*,bn-an≠0,
得
=
(n≥2).
∴数列{bn-an}是公比为
的等比数列.
(3)解:由(2)得bn-an=
·(
)n-1,
∴bn=
+
·(
)n-1(n∈N*).
∵b1-a1+b2-a2+…+bn-an=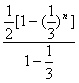
,
∴b1+b2+…+bn-(a1+a2+…+an)= 
［1-(
)n］.
∴Tn
=
［1-(
)n］.
∴Tn=
+
［1-(
)n］(n∈N*).
练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn（a、b∈R），且S25=100，则a12+a14等于（ ）
| A、16 | B、8 | C、4 | D、不确定 |