题目内容

【题目】已知函数．

(I)求函数的对称轴方程；

(II)将函数的图象上各点的纵坐标保持不变，横坐标伸长为原来的2倍，然后再向左平移个单位，得到函数的图象．若分别是△ABC三个内角A，B，C的对边，a=2，c=4，且，求b的值．

【答案】（1）（2）

【解析】试题分析:（1）先利用二倍角公式、配角公式将函数化为基本三角函数形式： ，再根据正弦函数性质求对称轴，（2）先根据图像变换得到函数的解析式，由求出B.再由余弦定理求b的值．

试题解析：解：（Ⅰ）函数

令，解得，

所以函数的对称轴方程为；

（Ⅱ）函数的图象各点纵坐标不变，横坐标伸长为原来的2倍，得到函数

的图象，再向左平移个单位，得到函数的

图象，所以函数.

又△中， ，所以，又，

所以，则.由余弦定理可知，

，

所以

练习册系列答案
相关题目

【题目】有下列四种说法：

①命题“”为假，则、至少一个为假；

②命题“一次函数都是单调函数”的否定是“一次函数都不是单调函数”；

③动点到点 与到点的距离之和为2，则点的轨迹是焦点在轴上的椭圆；

④命题“若直线与双曲线相切，则该直线与双曲线只有一个公共点”的逆命题是真命题．

其中正确的有__________．（填写序号）

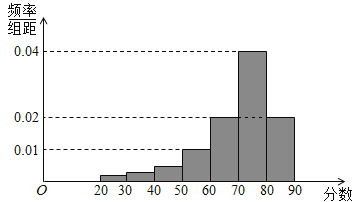
【题目】某经销商从外地水产养殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如下图：

（1）记事件为：“从这批小龙虾中任取一只，重量不超过35的小龙虾”，求的估计值；

（2）若购进这批小龙虾100千克，试估计这批小龙虾的数量；

（3）为适应市场需求，了解这批小龙虾的口感，该经销商将这40只小龙虾分成三个等级，如下表：

等级

一等品

二等品

三等品

重量（）

按分层抽样抽取10只，再随机抽取3只品尝，记为抽到二等品的数量，求抽到二级品的期望．

【题目】已知函数f（x）= ．
（1）用定义证明函数f（x）在（﹣∞，+∞）上为减函数；
（2）若x∈[1，2]，求函数f（x）的值域；
（3）若g（x）= ，且当x∈[1，2]时g（x）≥0恒成立，求实数a的取值范围．

【题目】已知椭圆的上、下焦点分别为，上焦点到直线 4x+3y+12=0的距离为3，椭圆C的离心率e=．

(I)若P是椭圆C上任意一点，求的取值范围；

(II)设过椭圆C的上顶点A的直线与椭圆交于点B(B不在y轴上)，垂直于的直线与交于点M，与轴交于点H，若，且，求直线的方程．

【题目】某校高三共有800名学生，为了解学生3月月考生物测试情况，根据男女学生人数差异较大，从中随机抽取了200名学生，记录他们的分数，并整理得如图频率分布直方图．

（1）若成绩不低于60分的为及格，成绩不低于80分的为优秀，试估计总体中合格的有多少人？优秀的有多少人？

（2）已知样本中有一半的女生分数不小于80，且样本中不低于80分的男女生人数之比2:3，试估计总体中男生和女生人数的比例．

【题目】已知函数y=f（x）是定义在R上的奇函数，当x＜0时，f（x）=x+2，那么不等式2f（x）﹣1＜0的解集是 ．

【题目】已知是椭圆的左右焦点，为原点， 在椭圆上，线段与轴的交点满足.

（1）求椭圆的标准方程；

（2）过椭圆右焦点作直线交椭圆于两点，交轴于点，若，求.

【题目】为了展示中华汉字的无穷魅力，传递传统文化，提高学习热情，某校开展《中国汉字听写大会》的活动．为响应学校号召，2（9）班组建了兴趣班，根据甲、乙两人近期8次成绩画出茎叶图，如图所示，甲的成绩中有一个数的个位数字模糊，在茎叶图中用表示．（把频率当作概率）．

（1）假设，现要从甲、乙两人中选派一人参加比赛，从统计学的角度，你认为派哪位学生参加比较合适？

（2）假设数字的取值是随机的，求乙的平均分高于甲的平均分的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网